无人驾驶系统是一个多传感器整合的系统,需要将不同位置的传感器数据统一到一个固定的坐标系——自车坐标系下,才能分析当前无人车所在的道路场景。本文将会集中在如何将传感器坐标系下的数据转换到自车坐标系下。有关无人驾驶技术中传感器到车体坐标系的坐标转换原理及数学推导,该原理不仅用在无人车领域,同时在机器人、无人机、三维建模等领域也得到了广泛使用。
无人车上拥有各种各样的传感器,每个传感器的安装位置和角度又不尽相同。对于传感器的提供商,开始并不知道传感器会以什么角度,安装在什么位置,因此只能根据传感器自身建立坐标系。无人驾驶系统是一个多传感器整合的系统,需要将不同位置的传感器数据统一到一个固定的坐标系——自车坐标系下,才能分析当前无人车所在的道路场景。
无人车的自车坐标系
不同的无人驾驶团队对于坐标系的定义可能不同,但这并不影响开发,只要团队内部达成一致即可。
以百度Apollo提供的自车坐标系为例,自车坐标系的定义为:
z轴 – 通过车顶垂直于地面指向上方
y轴 – 在行驶的方向上指向车辆前方
x轴 – 自车面向前方时,指向车辆右侧
车辆坐标系的原点在车辆后轮轴的中心,如下图所示。
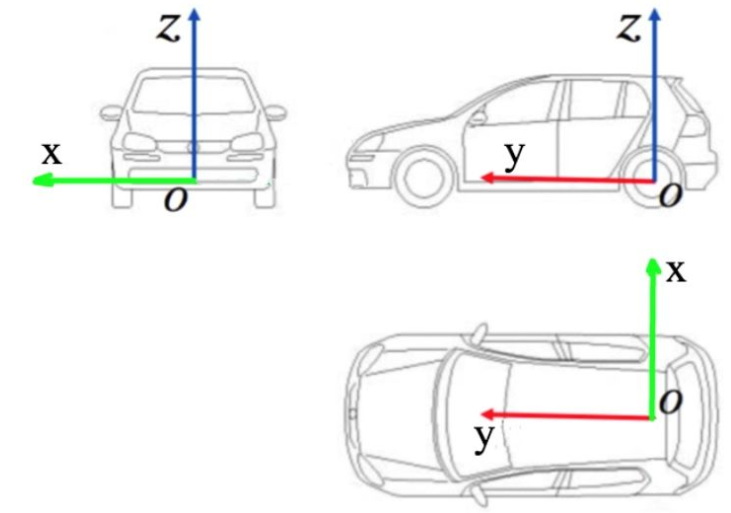
传感器坐标系与自车坐标系的转换
对于无人车的传感器安装位置,业内大同小异,比如奥迪A8的传感器配置如下图所示:
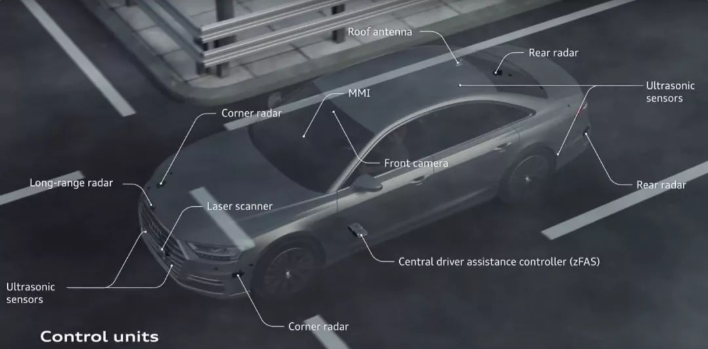
以安装在无人车左前方的角雷达(Corner radar)为例,进行后面的介绍,叫雷达的安装位置和坐标系如下图绿线所示。
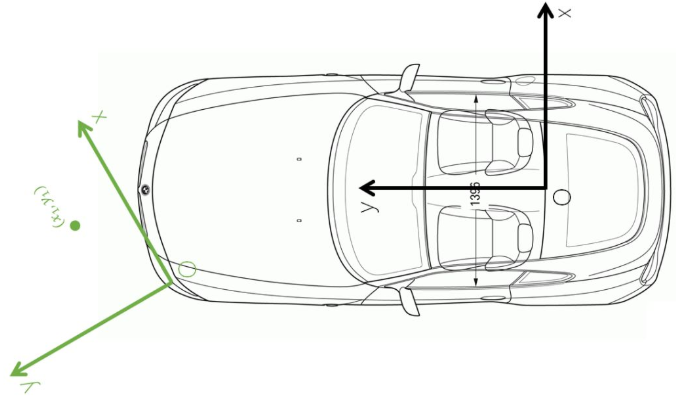
角雷达检测到的障碍物如图中的绿点所示,绿点在雷达坐标系下的坐标为(x1,y1),为了便于理解暂不加入z方向的坐标。
绿点转换到自车坐标系下需要经过一定的数学运算。基本思路是这样的:
| 平移
先将角雷达坐标系的O点平移到与自车坐标系的O点重合,此时(x1,y1)需要减去两个坐标系在x和y方向的距离。如下图所示:
| 旋转
在两个坐标系的O点重合后,将角雷达坐标系沿着z轴进行一定角度的旋转,这样(x1,y1)就转到了自车坐标系上。这个过程在数学上称为欧拉旋转。
坐标系的平移和旋转是两件相互独立的事情,先平移再旋转和先旋转再平移并不会影响最终的结果。
以上是感性的分析过程,下面我们将这整个过程在数学上实现。
| 平移
平移步骤根据传感器安装位置和自车后轴的距离进行计算,仅仅是XYZ三个方向加减运算。
| 旋转
绕轴旋转需要引入角度,不是简单的加减运算,所以我们通过图示来推导一下。
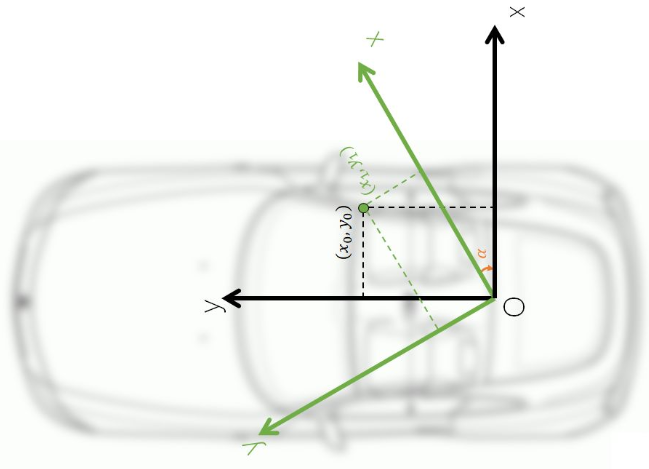
先将两个坐标系变换到正常的视角,如下图所示:
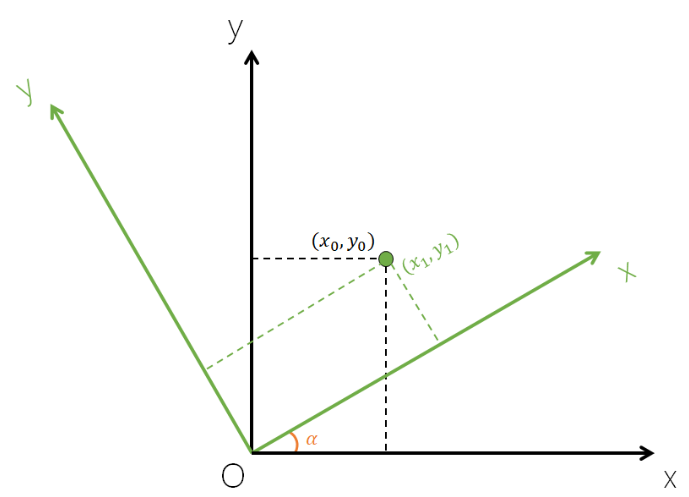
障碍物在角雷达坐标系下的坐标为(x1,y1),假设障碍物在自车坐标系下的坐标为(x0,y0),需要根据安装角度α(可测量),用x1,y1,α这三个已知量表示x0,y0,求得他们的数学关系。
通过做辅助线进行计算,如下图蓝线所示所示:
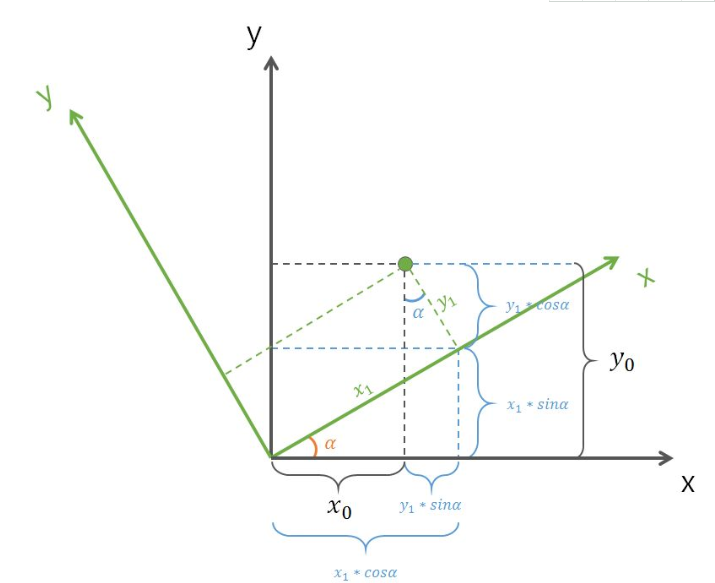
何关系可用以下两个等式表示:
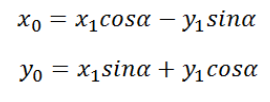
使用矩阵表示,可以简化表达,可以用一个等式代替两个等式,是这样的
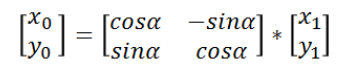
于这次旋转是绕z轴旋转,因此旋转前和旋转后的z值是保持不变的
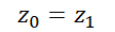
将z方向的值也放到上面的等式中,即可得到
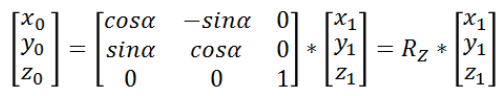
就意味着,只要把角雷达采集到的障碍物坐标值与上面这个矩阵进行矩阵乘法运算,即可完成沿Z轴的旋转。在这里我们把这个矩阵叫做Z轴旋转矩阵RZ,那必然还有沿着X轴和Y轴的旋转矩阵RX和RY。
角雷达目标的坐标依次右乘这三个矩阵,就完成了沿着Z轴,Y轴,X轴的旋转,得到的结果就是自车坐标系下的坐标值了。即
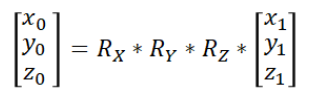
再加上一个平移的矩阵,就能够完整描述整个坐标转换的关系了
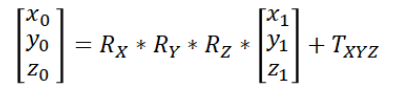
不同的坐标系定义,会有不同的RX,RY和RZ,因此需要根据实际情况计算旋转矩阵和平移矩阵。
欧拉旋转所存在的问题
以上过程也称为欧拉旋转,但是欧拉旋转会有一个不可避免的问题——万向锁。欧拉旋转的过程中在某些特殊情况时,会导致丢失维度。万向锁通过文字解释起来会有点困难,可以看一个讲解万向锁的小视频进行了解。
视频出处:
为了解决欧拉旋转所带来的万向锁问题,业界引入了四元数。四元数除了解决万向锁的问题外,还能在一定程度上简化计算。因而百度Apollo也选择了四元数作为各个传感器安装位置和角度的存储介质。有关四元数的定义和使用方法这里不做详细讨论,可参看Apollo的Calibration模块。
结语
实际参与到开发中你才会发现,自己在大学学习的高数和线性代数等都是很重要的数学工具,而不是仅仅用来考试的。
以上就是有关无人驾驶技术中传感器到车体坐标系的坐标转换原理及数学推导,该原理不仅用在无人车领域,同时在机器人、无人机、三维建模等领域也得到了广泛使用。
