我们先来说说电容,都说大电容低频特性好,小电容高频特性好,那么根据容抗的大小与电容C及频率F成反比来说的话,是不是大电容不仅低频特性好,高频特性更好呢,因为频率越高,容量越大,容抗就越低,高频就是否越容易通过大电容呢,但从大电容充放电的速度慢来说的话,高频好象又不容易通过的,这不很矛盾吗?
首先,高频低频是相对的。如果频率太高,那么,电容的容量变得再大也没有意义,因为,大家知道,线圈是电感,是阻高频的,频率越高,阻碍作用越大。尽管电感量很小,但是,大容量电容一般都有较长的引脚和较大的极板圈在一起,这时,电容两脚的等效电感量已经对高频起了很大的阻碍作用了。

因此,高频不容易通过高频性能差的大容量电解电容,而片状的陶瓷电容则在价格性能上占尽优势。
同理,是不是电感越大对高频了阻碍作用越大呢?不是。为了得到较大的电感量,必须有尽可能多、尽可能大的线圈,而这些导体就向电容的无数个极板,如果碰巧这些极板间距又较近的话(这是追求多圈数无法避免的),分布电容会给高频信号提供通路。
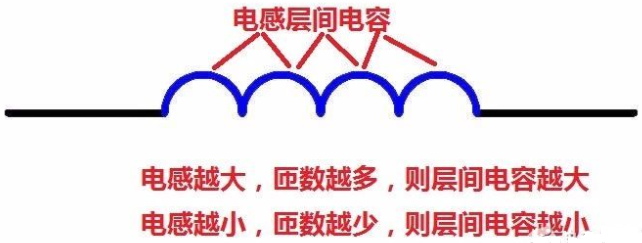
所以,不同频段的信号要选用合适容量的电容和电感。
下面咱们一起把最常用的三个无源器件,电阻、电容、电感的高频等效电路分析一下:
1、高频电阻
低频电子学中最普通的电路元件就是电阻,它的作用是通过将一些电能装化成热能来达到电压降低的目的。电阻的高频等效电路如图所示,其中两个电感L模拟电阻两端的引线的寄生电感,同时还必须根据实际引线的结构考虑电容效应;用电容C模拟电荷分离效应。
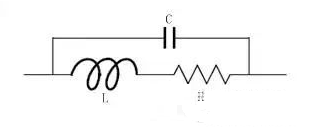
电阻等效电路表示法
根据电阻的等效电路图,可以方便的计算出整个电阻的阻抗:

下图描绘了电阻的阻抗绝对值与频率的关系,正像看到的那样,低频时电阻的阻抗是R,然而当频率升高并超过一定值时,寄生电容的影响成为主要的,它引起电阻阻抗的下降。当频率继续升高时,由于引线电感的影响,总的阻抗上升,引线电感在很高的频率下代表一个开路线或无限大阻抗。
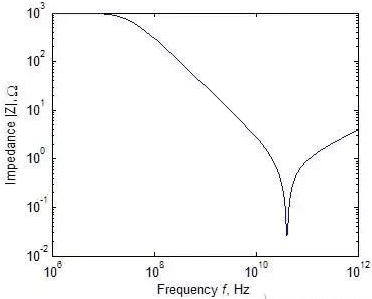
一个典型的1KΩ电阻阻抗绝对值与频率的关系
2、高频电容
片状电容在射频电路中的应用十分广泛,它可以用于滤波器调频、匹配网络、晶体管的偏置等很多电路中,因此很有必要了解它们的高频特性。电容的高频等效电路如图所示,其中L为引线的寄生电感;描述引线导体损耗用一个串联的等效电阻R1;描述介质损耗用一个并联的电阻R2。
电容等效电路表示法
同样可以得到一个典型的电容器的阻抗绝对值与频率的关系。如下图所示,由于存在介质损耗和有限长的引线,电容显示出与电阻同样的谐振特性。
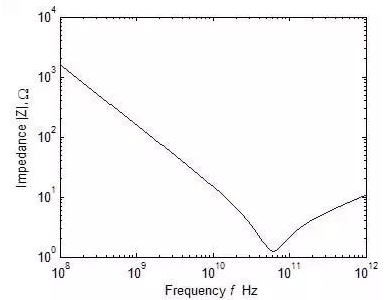
一个典型的1pF电容阻抗绝对值与频率的关系
3、高频电感
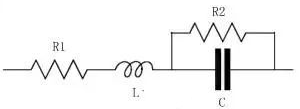
电感的应用相对于电阻和电容来说较少,它主要用于晶体管的偏置网络或滤波器中。电感通常由导线在圆导体柱上绕制而成,因此电感除了考虑本身的感性特征,还需 要考虑导线的电阻以及相邻线圈之间的分布电容。电感的等效电路模型如下图所示,寄生旁路电容C和串联电阻R分别由分布电容和电阻带来的综合效应。

高频电感的等效电路
与电阻和电容相同,电感的高频特性同样与理想电感的预期特性不同,如下图所示:首先,当频率接近谐振点时,高频电感的阻抗迅速提高;第二,当频率继续提高时,寄生电容C的影响成为主要的,线圈阻抗逐渐降低。
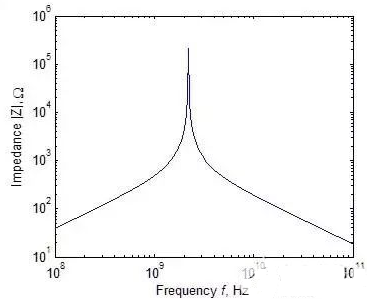
电感阻抗绝对值与频率的关系
总之,在高频电路中,导线连同基本的电阻、电容和电感这些基本的无源器件的性能明显与理想元件特征不同。读者可以发现低频时恒定的电阻值,到高频时显示 出具有谐振点的二阶系统相应;在高频时,电容中的电介质产生了损耗,造成电容起呈现的阻抗特征只有低频时才与频率成反比;在低频时电感的阻抗响应随频率的增加而线形增加,达到谐振点前开始偏离理想特征,最终变为电容性。这些无源元件在高频的特性都可以通过前面提到的品质因数描述,对于电容和电感来说,为了调谐的目的,通常希望的到尽可能高的品质因数。
