在分析了三线制平衡电桥法的基础上,提出了测量电路模型,描述了消除导线电阻的测量方法,分析了提高测量精度的措施,推导出了数字校准公式。使用通用运算放大器OP07与14位分辨率双积分型A/D转换器ICL7135设计了简洁的输入检测电路。经实验验证,该电路对于Pt100热电阻,导线电阻在0~20 Ω范围内,热电阻测量误差将优于±0.1%。
热电阻传感器是一种电阻值随环境温度变化而改变的温度传感器,其中用金属铂做成的热电阻因具有稳定性好、精度高、测温范围大等优点,而被广泛应用。测量温度的热电阻测温仪主要由热电阻传感器、测量显示仪表及连接导线组成。由于热电阻传感器自身的温度灵敏度较低,连接导线所具有的线路电阻对测量结果影响不容忽视,为了消除导线电阻的影响,热电阻测温仪广泛采用平衡电桥式三线制接法,这种方法使温度误差得到一定的补偿,但线路电阻的影响依然存在。提出基于恒压分压式三线制导线电阻补偿方法,电路简单,实现方便,可完全消除导线电阻的影响。相比于文献所提出的使用较多的硬件电路进行导线电阻补偿方法,该方法具有更加简洁的导线电阻补偿电路。
1 常用热电阻测量方法分析
对于Pt100铂热电阻,国际温标BS-90中给出其阻值随温度变化关系如式(1)所示。
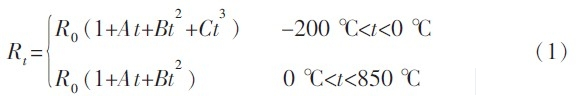
式中,Rt为热电阻在温度为t℃时的阻值,R0为热电阻在温度为0℃时的阻值,R0=100 Ω,A=3.968 47×10-3℃-1,B=-5.847x10-7℃-2,C=-4.22x10-12℃-3是与传感器自身相关的系数。
由式(1)可知,Pt100热电阻的灵敏度约为0.38 Ω/℃,为减小连接导线的线路电阻对测量结果的影响,一般常用三线制电桥法进行测量。VR=1 V其电路原理如图1所示。Rt为测温电阻,r为连接导线电阻,R1、R2、R3为固定桥臂,R1=R2=1 000 Ω,R3=100 Ω,VR为基准参考电压,G为测量仪表。在该电路中,3根导线分别连接传感器桥臂、电阻桥臂和输出端。采用这个方法可以很容易地测出待测电阻Rt。但是,在实际使用时,温度传感器和测温电路之间往往有一定距离,连接导线的电阻率约为0.1~0.5 Ω/m,连接导线电阻r所引起的测量误差不能忽视。
如图1所示的电桥,在不考虑线路电阻r时,电桥的输出为:V‘c=VRRt/(R1+Rt)-VRR3/(R2+R3),考虑线路电阻时,电桥输出Vc=VR(Rt+r)/(R1+Rt+r)-VR(R3+r)/(R2+R3+r),假设电桥在Rt=Rx时电桥平衡,即R2Rx=R1R3,且满足桥臂电阻R1=R2=R3=Rx=R,当Rt发生△R变化时,即Rt=R+△R,可计算出此时电桥因线路电阻r的存在造成的误差为:
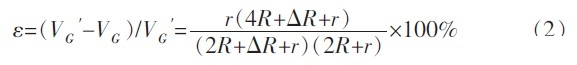
可以看出导线电阻r影响Rt的测量结果,并且无法通过调零电路完全消除。基于以上分析,提出了一种可完全消除导线误差的恒压分压式三线制高精度前置电路。
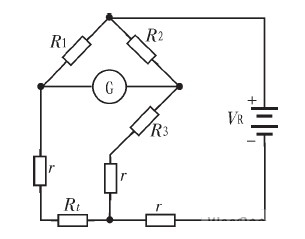
图1 三线制平衡电桥法测量原理图
2 恒压分压式三线制测量电路
2.1 测量原理
这里所使用的恒压分压式三线制法测电阻可以排除导线电阻的干扰,其等效原理图如图2所示。其中Rt为热电阻。r为导线等效电阻。VR为基准参考电压,VAD是A/D转换器的参考电压,β为电压放大倍数。
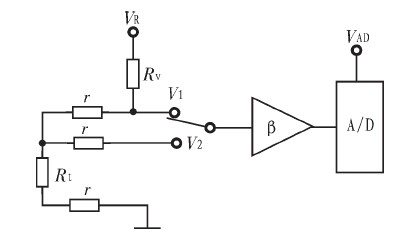
图2 恒压分压式三线制法测量原理图
由欧姆定律可得基本关系式:
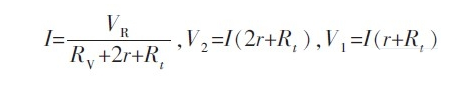
由以上关系式可计算出:
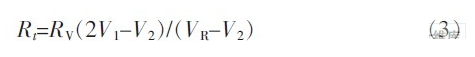
从式(3)可以看出:在已知RV和VR的情况下,欲求Rt只需测出V2和V1,而与导线电阻r没有关系。且测量精度只取决于RV的精度与V1,V2的测量精度。在电桥法中无法消除的导线电阻在恒压分压式三线制方法中被完全消除。
由于热电阻当有电流通过时,会引起自身温度升高,所以必须考虑其本身自热误差,即必须考虑流过热电阻的电流所引起的升温误差。常用的Pt100热电阻驱动电流约为1 mA。0℃时相当于自热功率约0.1 mW,在高精度测量时,应进一步降低自热功率,减小自热误差。这里设置VR=2.5V,RV=10kΩ,则自热功率约为0.006 mW。
2.2 提高测量精度措施
与三线制平衡电桥法相拟,图2所示的电路输出电压V1与V2数值较小,还应加入一级电压放大后,再进行A/D转换。参考电压VR一般由精密恒压源提供稳定的电压信号,此外单片机软件在数学计算上选择适当的算法和字长时,该计算误差也可不计。但放大电路的放大倍数β和RV会因元器件个体而异,特别是在批量生产时元器件的精度难以保证统一,因此对一个具体输入电路而言,还需考虑β和RV带来的误差。
为了消除β和RV带来的误差,可以通过标定法,在仪表生产时进行自动标定计算,求得实际电路的β和RV值,再将这两个参数记录在仪表的非易失存储器中,在仪表进行温度测量时,读取该参数按式(1)进行计算,从而得到精确的测量温度。
如果把图2中长导线用尽可能短的导线代替(即r=O),并以精密电阻R代替热电阻Rt,VAD是A/D转换器的参考电压,β为电压放大倍数,其余部分保持不变,则有:
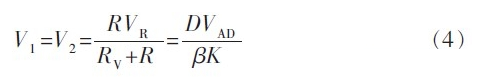
在式(4)中,R是已知阻值的精密电阻;D是A/D转换的结果,该结果可方便地从仪表显示装置中读出;VR与VAD是基准电压,为恒定的常量;β为电路的总放大倍数;K是A/D转换的比例因子,如对于14位的A/D转换器,K=214。那么式(2)中只有2个未知数RV和β。对于一个具体输入电路,如果取2个阻值已知的精密电阻R1、R2分别接入图2所示电路进行标定(标定时,尽量使r=0),就可以得到一个二元一次方程组。这样,对于一个具体输入电路而言,可从方程组解出β和RV,其结果如下:
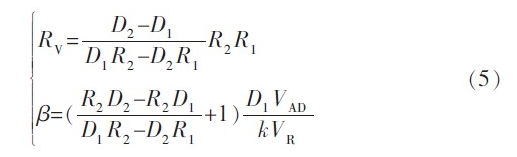
上述标定方法可以总结为:2个阻值已知的精密标准电阻R1、R2分别接仪表的输入端,且使用连接导线的电阻尽量减小,这时记录仪表读数D1与D2,代入式(5)即可计算出所标定仪表的未知参数β和RV。在使用中,建议将VR与VAD使用同一个基准源,这样式(5)中β的计算就与参考电压的精度无关。这种方法减小了不同基准源之间的差异,特别是减小了不同基准的时漂与温漂的影响。
2.3 测量电路
图3是高精度Pt100温度测量系统的前置输入电路部分,其中Pt100基准电压与A/D转换器ICL7135的基准电压为同一电压基准源,Pt100的2路测量输入信号V1与V2采用同一运算放大器放大(1+R3/R4)倍后进入A/D转换器,使用微型继电器K1进行通道选择,这种方法共用运算放大器、A/D转换器、基准电压源,减小了不同器件之间的差异对测量结果的影响。ICL7135的A/D转换结果通过串行方式与单片机相连,可以大大节约单片机的IO口。该电路在标定时,使用标准电阻100Ω与300Ω进行标定,将标定结果β和RV存入单片机系统的EEPROM中。在实际测量中,单片机系统将β和RV取出,作为已知值,由式(3)计算出电阻Rt值。
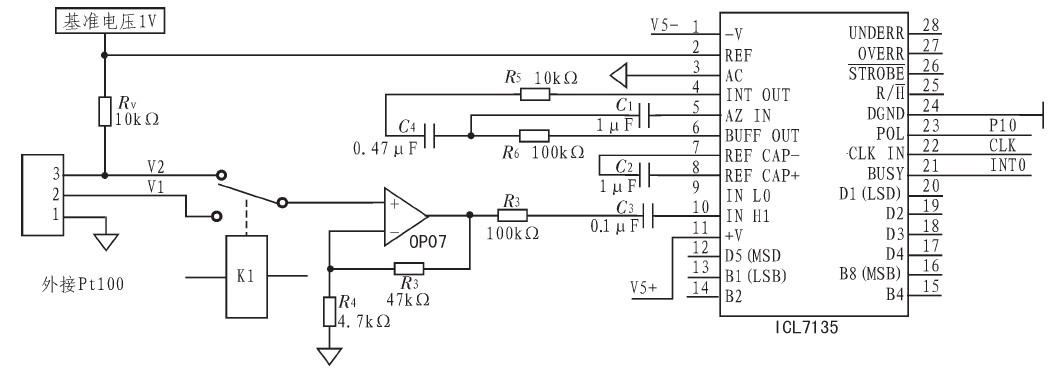
图3 恒压分压式三线制法测量及A/D转换电路
2.4 测量电路试验分析
对比三线制平衡电桥法,该电路检测结果得到了大大提高,表1是2种不同方法的测量标准电阻值的对比。其中r为线路电阻。
表1热电阻阻值测量结果
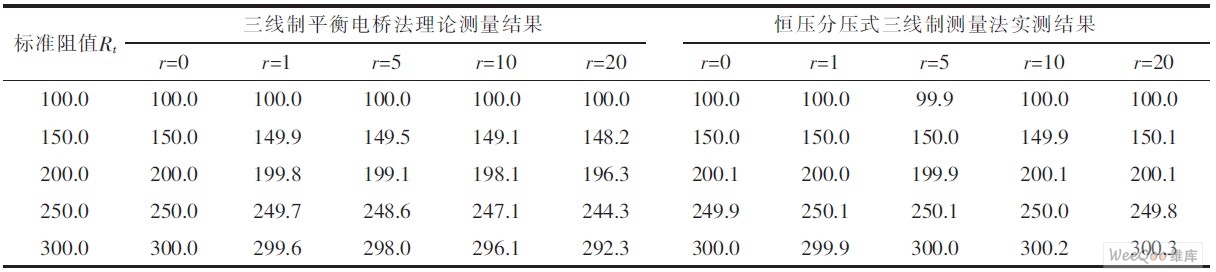
从表1中可以看出,由于三线制平衡电桥法理论测量结果即存在较大误差,且随线路电阻r的增加,引起的误差越大,随待测热电阻阻值增大,绝对误差也呈增大的均势。表1中,最大相对误差为被测电阻Rt=300 Ω,线路电阻r=20 Ω时,达到了2.57%。本文采用改进后的三线制法的实测结果在所测数据范围内最大绝对误差只有0.3 Ω,最大相对误差为±0.1%。电路使用的A/D转换器仅相当于14位的A/D转换精度,若使用更高精度的A/D转换器,可达到更高的测量精度。在实际的热电阻传感器测温仪表中,还需加入由被测电阻转换为对应温度的相关程序。即在测量得到Rt后,由式(1)计算即可精确求解出实际的温度值。
3 结论
三线制平衡电桥法在热电阻测量中应用广泛,但存在无法消除传感器引线电阻引起测量误差的问题。本文分析了测量热电阻平衡电桥法中存在的问题,提出了恒压分压式三线制测量方法,分析了测量电路产生误差的原因及影响因素,推导并建立了待测电阻的影响参数及公式,设计了完整的测量电路,包括信号放大器和A/D转换器以及与单片机的接口电路。最终对所设计电路的测试精度进行试验测定,试验表明,三线制平衡电桥法测标准电阻值在100~300Ω,线路电阻在0~20Ω时最大测量误差达到2.57%,而平衡三线制测量误差只有±0.1%。从而获得了高精度的三线制热电阻测量电路。
