无线传感器网络作为一门新兴的技术,被应用于广泛的领域中。而基于接收信号强度指示(RSSI)应用的无线传感器网络,需要对网络中接收到同一个节点的多个RSSI值进行滤波。为了对RSSI滤波有一个全面的认识,介绍了几种滤波方法,详细综述了每种滤波方法的原理和特点,最后指出应根据具体情况,权衡滤波效果、算法复杂度、节点能耗等各方面因素,选择一种或者多种算法混合的滤波方法。
0 引言
无线传感器网络(WirelessSensor Network,WSN)就是由部署在特定监测区域内大量的廉价微型传感器节点组成,通过无线通信方式形成的一个多跳自组织网络系统,它作为一种全新的信息获取和处理技术,在目标跟踪、环境监测、军事应用、医疗卫生、空间探索等领域都有着广泛的应用,节点定位技术是无线传感器应用的基础,常用的节点定位技术都是基于RSSI的,节点之间通过接收到的RSSI 值,利用经验公式转换为距离,再通过适当的算法计算出节点坐标位置。然而,由于环境中往往存在多径、散射、障碍物、电磁干扰等不稳定因素,使得RSSI值不稳定,具有较大的波动性。实际使用中,需要对测得的多个RSSI值进行滤波优化处理,得到优化后的RSSI值,再进行定位计算。下面分别介绍几种常用的RSSI滤波方法。
1 RSSI 滤波方法
1.1 均值滤波
均值滤波是指节点接收到另一节点的多个RSSI值之后,求其算式平均值,作为测试结果,如式(1)所示:
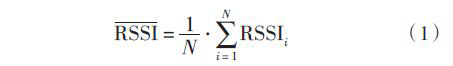
该方法简单,易实现。当样本容量很大,RSSI波动范围较小时,信号平滑度较高,可较好地解决RSSI干扰问题;当RSSI值波动较大时,该方法可信度下降。
1.2 递推平均滤波
递推平均滤波是把连续接收到的N 个RSSI值看成一个队列,队列的长度固定为N,每次接收到一个新的RSSI值后放入队尾,并扔掉原来队首的一个RSSI值。最后把队列中的N 个数据进行算术平均运算,就可获得新的滤波结果。该滤波算法优点是对周期性干扰有良好的抑制作用,平滑度高,缺点是对偶然出现的脉冲性干扰抑制作用差,不易消除由于脉冲干扰所引起的采样值偏差,不适用于脉冲干扰比较强的场合。
1.3 中位值滤波
中位值滤波是指采集N(N 为奇数)个RSSI值之后,将这N 个RSSI值按大小顺序排列,取其正中间的RSSI值作为滤波输出,如式(2)所示:

中位值滤波能有效克服因偶然因数引起的波动干扰,但是对于脉冲干扰比较强,样本容量不多的情况下,滤波效果不理想。
1.4 狄克逊检验法滤波
狄克逊检验法滤波是通过极差比判定和剔除异常数据。该方法认为异常数据应该是最大数据和最小数据,因此该方法是将数据按大小排列,检验最大数据和最小数据是否是异常数据。以样本容量小于等于30为例,具体步骤如下:
(1)将对同一节点多次测量到的RSSI 值按从小到大的顺序排列,{RSSI(1),RSSI(2),RSSI(3),-,RSSI(n - 2),RSSI(n - 1),RSSI(n)} ,并确定检出水平 α =0.05;(2)根据狄克逊统计公式[10]有:
当n=3~7时检验高端异常值:

(3)根据检出水平α ,查狄克逊检验的临界值表,在狄克逊检验法的临界值表中查出对应α ,n 的临界值D(α,n) .
(4)当rij ﹥ rij- ,且rij ﹥ D(α,n) 时,RSSI(n) 为异常值;当rij- ﹥ rij ,且rij- ﹥ D(α,n) 时,RSSI(1) 为异常值;否则判断未发现异常值。
(5)去除异常值后,对剩下的样本数据,重复执行步骤(1)~步骤(5),直到不再检出异常值为止。最后剩下的数据可求其算数平均值作为最后滤波输出。
狄克逊检验法能够有效地去除样本中的异常值,但需要查表,通常与其他的滤波算法混合滤波。
1.5 高斯滤波
对同一个节点接收到的多个RSSI值中,由于各种干扰,必然存在由误差引起的小概率事件,通过高斯模型选取高概率发生区的RSSI值作为有效值,再求其几何平均值,这种方法能够有效地减少小概率、大干扰对整体测量数据的影响,提高定位的准确性。
RSSI服从(0,δ2)的高斯分布,其概率密度函数为:

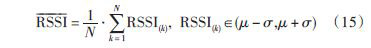
高斯模型解决了RSSI在实际测试中易受干扰、稳定性差等问题,提高了定位精度,但对阴影效应、能量反射等长时间干扰问题处理效果欠佳。
1.6 速度常量滤波
基于物体在一定范围内的移动并不是任意的,当前位置和前一时刻的位置存在一种相互关系的思想,采用速度常量,使移动点保持匀速运动,算法描述如下:
估计值:

预测值:
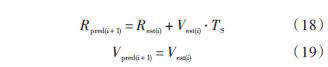
式中: Rprev(i) 为i 时刻信号强度的测量值;Rpred(i) 为i 时刻信号强度的预测值;Rest(i) 为i 时刻信号强度滤波值;Vest(i)为i 时刻信号强度变化率的滤波值;Vpred(i) 为i 时刻信号强度变化率的预测值;a,b 为增益常量;TS 为采样时间间隔。基于速度常量的滤波算法能够有效地减小信号波动给测量带来的影响。
1.7 卡尔曼滤波
卡尔曼滤波的基本思想是:以最小均方误差为最佳估计准则,采用信号与噪声的状态空间模型,利用前一时刻的估计值和当前时刻的观测值来更新对状态变量的估计,求出当前时刻的估计值,算法根据建立的系统方程和观测方程对需要处理的信号做出满足最小均方误差的估计。
RSSI用xk 表示,采样过程的数学模型可以表示为一个高斯白噪声序列驱动的一阶自递推过程,其状态方程和观测方程可表示为:
状态方程:

卡尔曼滤波能在一定程度上削弱由于噪声叠加造成的RSSI观测值偏离,经过卡尔曼算法处理后的RSSI值,稳定性更好。卡尔曼在目标跟踪方面也能取得很好的效果。
2 结语
以上论述了几种常用的RSSI滤波处理方法、原理,各种算法都有各自的特点,没有哪一种是绝对最优的,比如均值滤波,其算法简单,易实现,但是精度不高,处理效果不佳,而高斯滤波处理效果好了很多,但是实现起来变得复杂一些,节点消耗更多能耗,同时占用了更多内存空间。实际应用中要根据具体情况,均衡各方面需求,选择合适的滤波方法,也可多种算法混合使用,以达到最佳的滤波效果。希望本文能够为无线传感器网络中处理RSSI值的相关研究者提供一些参考和借鉴。
