摘要：为了对付现代战争的“四大威胁”，采用分布式、多制式传感器组网对敌方目标进行探测已经变得十分必要，而多制式传感器组网的关键技术之一是数据融合问题。分析了三坐标雷达、两坐标雷达和红外探测器这三种常见种类的传感器点迹几何模型，提出了一种针对这三种不同制式传感器的数据融合算法，并在某工程中得到了成功应用。
关键词：多制式；测量相关；航迹相关；数据融合
0 引言
将不同制式的传感器采用分布式、组网探测的方式能够有效对付现代战争的“四大威胁”。在分布式组网探测系统中，通常采取如下方式进行处理：首先由各个探测器形成局部航迹；然后将航迹数据上报到上级情报中心；最后情报中心对各局部航迹进行数据融合得到一个次优的融合航迹。多种传感器的目标关联方法主要有两种方案，一种是测量一航迹关联方案；另一种是航迹一航迹关联方案。
本文在此分析讨论的航迹一航迹关联算法，适用于包含有三坐标雷达、两坐标雷达和红外探测器这三种传感器组成的分布式网络处理系统。在该分布式处理系统中，各个探测器先各自形成独立的局部航迹，然后将航迹数据上报到情报融合中心进行数据融合处理并最终形成融合航迹。情报融合中心数据处理的难点在于有三种探测器测量值形式各不相同，除三坐标雷达的局部航迹可以提供状态估计以外，另外两种传感器都仅能提供每条局部航迹对应的测量集。
1 模型建立与分析
下面以三种探测值的几何模型为基础定义测量一测量间的距离，在此基础上进一步定义了测量集一测量集间的距离，并作为航迹一航迹关联的定量度量。通过这种处理后，航迹关联问题被转化为了单纯的聚类问题。在状态估计上本文采用数据压缩方式。即先用极大似然估计法从相关的多个测量数据中估计出融合点迹中心，最后用卡尔曼滤波器组得出最终的融合航迹。
1．1 三坐标探测器点迹的几何模型
三坐标雷达的测向量为z=(r,θ,φ)，其中r为斜距，θ为方位角，φ是高低角。三坐标雷达点迹测量几何模型如图1所示。
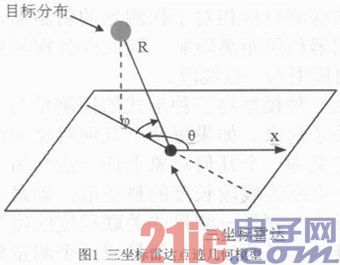
三坐标雷达的一次测量能够确定目标在z=(r，θ，φ)所代表的点的附近，因此其测量点迹的几何模型为一个点。
1．2 两坐标雷达点迹几何模型
两坐标雷达的测向量形如z=(r，θ，φ)，其中r为斜距，θ为方位角。两坐标雷达点迹几何模型如图2所示。
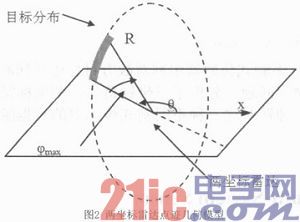
两坐标雷达只能探测到斜距和方位角，通过其测量只能确定目标在一个位于竖直平面内的半径为r的圆弧附近。并且受两坐标雷达高低角探测范围限制，所以两坐标雷达的测量点迹的几何模型为一段弧线。
1．3 红外探测器点迹几何模型
红外探测器则是测向量形如z=(r，θ，φ)。其中θ为方位角，φ是高低角。红外探测器点迹测量几何模型如图3所示。
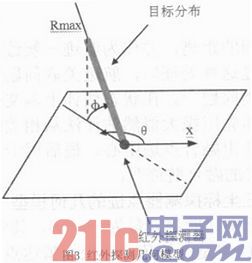
红外探测器可以准确探测目标方位角和高低角，但却无法探测目标相对于探测器的斜距离，并且受红外探测器作用距离限制。因此红外探测器的测量点迹几何模型为一直线段。
以上三种模型将三种形式的探测量与三种几何对象相关了起来。如果每两个几何对象问的最小几何距离定义为一个几何对象上任一点到另一几何对象上任一点所连线段长度的最小值，则最小几何距离就可以作为测量一测量的关联程度的度量。度量相似程度是为了确定两个测量或两个测量集是否来自于同一个目标。
通过分析，不难发现共有六种度量情况：1)点到点；2)点到弧线段；3)点到直线段；4)直线段到直线段；5)弧线段到弧线段；6)弧线段到直线段。其中，1)～4)种情况都很容易找到对应的数学公式直接求解；而对于5)和6)这两种情况，虽不能用简单的方法求解，但是可以通过最陡下降法等数值最优化方法求解。下面就以测量间的最小距离为基础，对两两测量集间的相似程度进行度量。
2 航迹关联算法
2．1 测量-测量相似程度的度量算法
测量-测量相似程度的最佳度量应该是两次探测间的统计距离。但由于存在非线性关系，真实的统计距离求取困难。而两次探测间的几何距离则容易求出。不同探测器在同一时刻对于同一目标的两个探测值之间的几何距离必定总是较小的，而对于不同目标的探测值之间的几何距离则不可能表现出这种特性。所以在较宽松的情况下，可以用以几何距离作自变量的某一函数作为近似的度量函数。
本文算法中，设来自两探测器在同一时刻对同一目标的两个探测值i和j间的几何距离为dij，假定dij符合方差为
的某种分布，则定义归一化距离
作为测量一测量相似程度的度量。而σij的近似计算公式可表示为：
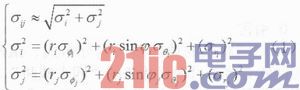
因红外探测器缺少距离量r，可用探测点迹对应直线段上取得最小距离dij的点的距离r’替代；因两坐标雷达缺少高低角量φ，可用探测点迹对应弧线段上取得最小距离dij的点的高低角φ’替代。红外的和两坐标雷达的σφ都取0。
2．2 测量集-测量集相似程度的度量算法
最简单的度量值就是测量集中对应测量相似程度的均值，即
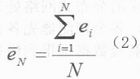
其中：ei为两测量集中第i时刻测量间的归一化距离，N为当前时刻。
考虑到探测器各自形成的局部航迹可能发生批号交换的错误，导致某一探测器同一批号的航迹前后半段来自不同的目标。因此，在进行数据融合时可能出现以下两种情况：1)两条航迹前半段来自同一目标，而后半段来自不同目标：2)两条航迹前半段来自不同目标，而后半段来自同一目标。如果用测量相似度均值作为测量集相似程度的度量标准，则当局部航迹发生上述第一种错误后，已经相关的两条航迹不能及时分离；当局部航迹发生第二种错误后，航迹不能及时合并。为了解决这一问题，我们可以通过对“历史”加以衰减，使相似度主要依靠近期的测量值来确定的方法。即
其中ζ∈(0，1)为衰减系数。
ζ越大，则对“历史”衰减越慢。它对批号交换等情况能做出的反应也迟钝；ζ越小，则对“历史”的衰减越快。它对批号交换等情况能做出的反应也灵敏：作为极端情况，当ζ→1时，
，退化为测量相似度均值；当ζ→0时，
，即以当前测量的相似度作为整条航迹的相似度，显然它能对批号交换等情况能做出最快速的反应，但它也最容易受到随机因素的干扰。ζ的值要根据航迹特点并结合实际情况适当选取。
把各个航迹看作模式样本，两航迹测量集间的相似度作为这两个模式样本间的距离，于是航迹关联问题就已转化为聚类分析问题，有多种具体的聚类方法可供选择，这里不再赘述。
3 数据融合算法
基于最大似然估计准则的估计器是一种基本估计器。若未知矢量x(既可是确定的，也可是随机的)与观测值有如下关系：
z=g(x)+r (5)
则可用最大似然估计求出该矢量x。式中，r是一个与x无关，且具有已知概率密度函数fr(r)的随机矢量。最大似然估计准则选择出最可能的观测值z的，即fz|x(z|x)为最大的估计
。不管x的概率是什么，只要知道了观测误差的概率分布就可求出该估计。
对本文讨论的情况，对于同一个x存在一组探测{zi}，使f{z}|x({z}|x)取得最大值的就是最大似然估计。已知任意两次探测相互独立，各探测分量(r，θ，φ等)也相互独立，且服从正态分布，即有：
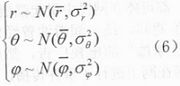
根据此条件可以求出f{z}|x({z}|x)和grad(Inf{z}|x)。再用梯度下降法即可求出使ln f{z}({Z})取得最大值的就是目标位置的最大似然估计值。
若上述测量集合{Zi}只包含一个两坐标探测器(两坐标雷达或红外探测器)点迹，则采用梯度下降法只能收敛到弧线段或直线段上，而无法收敛到一点。因此上面的估计只针对测量集合{Zi}至少包含两个探测器或包含三坐标雷达的探测系统的情况。
4 应用
在某项目研制中，应用本文所讨论的融合算法，三坐标雷达探得的目标和至少两个探测器同时探测得到的目标都能形成完整的三维融合点迹。而仅被一部两坐标探测器探测到目标的点迹集合无法通过前面的方法变成三维点迹。处理后的整个点迹序列表现为三维融合点迹和原始的二维点迹分段交替出现。为了得到最终的融合航迹，需选用一组恰当的卡尔曼滤波器组进行切换滤波。即当存在三维点迹时用探测值形式为(x,y,z)的卡尔曼滤波器进行滤波，当遇到无三维点迹时切换为两坐标探测器进行卡尔曼滤波，并且切换时沿用前一滤波器估计出的状态
向量和状态向量误差协方差作为滤波器的起始条件，由此就成功地融合出了完整的三维航迹，同时能很好地估计出目标速度和加速度。
5 结语
本文提出的多制式传感器数据融合算法能有效地解决多制式传感器系统中的数据融合问题；算法简单，易于工程实现。