数字电路分为组合逻辑电路和时序逻辑电路两类，组合逻辑电路的特点是输出信号只是该时的输入信号的函数，与别时刻的输入状态无关，它是无记忆功能的。这一章我们来学习组合逻辑电路。这一章是本课程的重点内容之一
我们在学习时把这一章的内容分为：
§4、1 逻辑电路的分析
§4、2 逻辑电路的设计
§4、3 常用的组合逻辑
§4、1组合逻辑电路的分析
一：组合逻辑电路的分析 （1）：有给定的逻辑电路图，写出输出端的逻辑表达式； （2）：列出真值表； （3）：通过真值表概括出逻辑功能，看原电路是不是最理想，若不是，则对其进行改进；
我们对组合逻辑电路的分析分以下几个步骤：
。 第一步：写逻辑表达式。我们由前级到后级写出各门逻辑表达式
例1：已知右面的逻辑电路图，试分析其功能。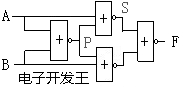
P=A+B S=A+P=AB W=B+P=AB
F=S+W=AB+AB
第二步：列真值表（如右图所示）。
第三步：逻辑功能描述并改进设计。
从真值表中可以看出这是一个二变量“同或”电路。原电路设计不合理，它只需一个"同或"门即可.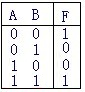
§4、2组合逻辑电路的设计
一：组合电路逻辑电路的设计
电路设计的任务就是根据功能设计电路，一般按如下的步骤进行：
（1）把逻辑命题换为真值表；这一步我们要从以下几个反面考虑
用英文字母代表输入或输出；
分清几个输入、输出；
分清输入和输出之间的对应关系。
（2）把逻辑函数进行化简，化简的形式则是根据所选用的逻辑门来决定；
（3）根据化简结果和所选定的门电路，画出逻辑电路图。
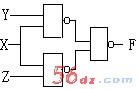
例：设计三变量表决器，其中X具有否决权。
第一步：列出真值表。（如右上图）
设X、Y、Z分别代表参加表决的变量；F为表决结果，
我们把变量规定为：X、Y、Z为1表示赞成；为0表示反对。
F为1表示通过；为0表示被否决。
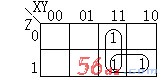
第二步：化简逻辑函数。
我们选用与非逻辑来实现。用卡诺图来化简（如右中图）F=
第三步：画逻辑电路。（如右图）
§4、3常用的组合逻辑
常用组合逻辑的种类很多，主要有全加器、译码器、编码器、多路选择器等，下面我们分别把它们介绍一下。
一：半加器和全加器
在数字系统中算术运算都是利用加法进行的，因此加法器是数字系统中最基本的运算单元。由于二进制运算可以用逻辑运算来表示，因此我们可以用逻辑设计的方法来设计运算电路。加法在数字系统中分为全加和半加（第一章我们已经介绍了）所以加法器也分为全加器和半加器。
（1）半加器设计
半加器不考虑低位向本位的进位，因此它有两个输入端和两个输出端。
设加数（输入端）为A、B ；和为S ；向高位的进位为Ci+1。
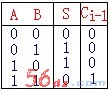
它的真值表为：如右图所示
函数的逻辑表达式为： S=AB+AB ； Ci+1=AB
逻辑电路图（用异或门和与门构成）为：如右图(2)所示
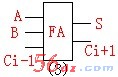
（2）全加器的设计（它的逻辑符号为图(3)所示）
由于全加器考虑低位向高位的进位，所以它有三个输入端和两个输出端。
设输入变量为（加数）A、B、 Ci-1，输出变量为 S、 Ci+1
它的真值表为：如图(4)所示
函数的逻辑表达式为：S=ABCi-1+ABCi-1+ABCi-1+ABCi-1=A
BCi-1
Ci+1=ABCi-1+ABCi-1+ABCi-1+ABCi-1=（AB）Ci-1+AB
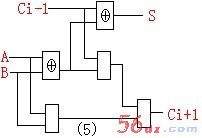
逻辑电路图(用异或和与门构成）为：如图(5)所示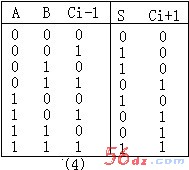
（3）全加器的应用
因为加法器是数字系统中最基本的逻辑器件，所以它的应用很广。它可用于二进制的减法运算、乘法运算，BCD码的加、减法，码组变换，数码比较等。
例 1：用全加器构成二进制减法器。
以四位二进制为例。（减法可转换为加补运算）
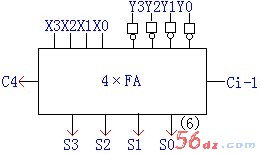
设两组四位二进制分别为X3X2X1X0和Y3Y2Y1Y0,把Y3Y2Y1Y0先进行求补然后再进行加法运算。
因为求补是逐位求反后再加“1”所以它的逻辑电路图为如图(6)所示:
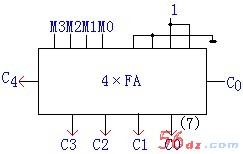
例 2：采用四位全加器完成8421BCD码转换为余3代码。
由于8421BCD码加0011即为余3代码，因此转换电路就是加法电路。
设8421BCD码四位又高位到低位为M3、M2、M1、M0，余3代码的四位由高到低为C3、C2、C1、C0。
它的逻辑电路图为如图(7)所示:
二：编码器和译码器
指定二进制代码代表特定的信号的过程就叫编码。把某一组二进制代码的特定含义译出的过程叫译码。
（1）编码器因为n位二进制数码有2n种状态，所以它可代表2n组信息。我们在编码过程中一般是采用编码矩阵和编码表，编码矩阵就是在卡诺图上指定每一方格代表某一自然数，把这些自然数填入相应的方格。
例 1：把0、1、2、...、9编为5421BCD码.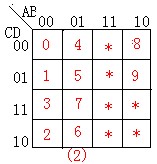
先来确定编码表如图(1)所示和编码矩阵如图(2)所示:
由编码表确定各输出端的逻辑表达式是：
A=5+6+7+8+9
B=4+9
C=2+3+7+8
D=1+3+6+8
根据这些表达式可用或门组成
逻辑电路如图(3)所示:
（2）：译码器编码的逆过程就是译码。
译码就是把代码译为一定的输出信号，以表示它的原意。实现译码的电路就是译码器。
译码器可分为二进制译码器、十进制译码器、集成译码器和数字显示译码驱动电路。其中二进制译码器是一种最简单的变量译码器,它的输出端全是最小项。
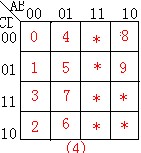
例 2：设计一译码电路把8421BCD码的0、1、2、...、9译出来.
四位二进制有十六种状态，而实际只需要十种，因此其余项作无关项考虑.
其编码矩阵为如图(4)所示.
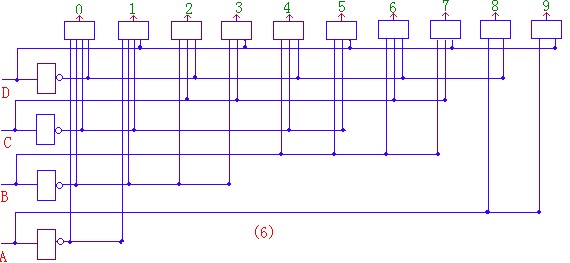
我们通过编码矩阵可得如下译码关系：如图(5)所示.
所以它的逻辑电路图为（用与门和与非门实现）
如图(6)所示:
集成译码器的工作原理与其它译码器一样，但它有它的特点.
它的特点为：
输入采用缓冲级;(减轻信号负载)输出为反码;低电平有效(减轻输出功率)增加了使能端.(便于扩展功能)
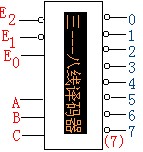
目前常用的典型的集成译码器是三------八译码器。
它的逻辑符号为.如图(7)所示:注：其中E0E1E2为使能端，只有当E1、E2为0时E0为1时此译码器才工作。
三：数据选择器和多路分配器
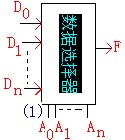（1）数据选择器它就是从多个输入端中选择一路输出，它相当于一个多路开关它的逻辑符号如图(1)所示:其中D0D1、、、Dn是数据输入端;A0A1、、、An为地址变量（有n个地址变量就有2n个输入端）.
常用的有二选一，四选一，八选一和十六选一，若需更多则由上述扩展。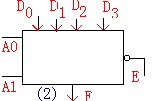
例 3：如图(2)所示的四选一数据选择器，试写出它的输出逻辑表达式和功能表
它的逻辑输出表达式为 F=（A0A1D0+A0A1D1+A0A1D2+A0A1D3）E
它的功能表为：如下表所示
从表上我们可以看出当使能端E为“1”时输出为“0”即禁止，只有当使能端为“0”时选择器才有效。
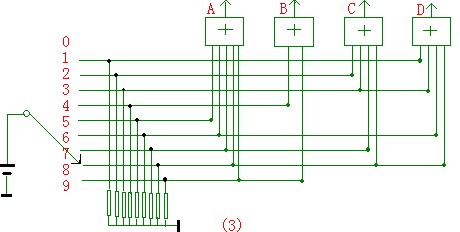
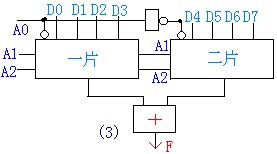
例 4：把四选一扩展为八选一。
地址
使能端
输入
输出
A0
A1
E
D
F
* *
1
*
0
0 0
0
D0---D3
D0
0 1
0
D0---D3
D1
1 0
0
D0---D3
D2
1 1
0
D0---D3
D3
八选一要有八个输入变量，因此需要三个地址变量(我们把其中一个A0作为使能段)；
四选一只能有四个输入变量，所以我们需要两个四选一和一个非门.非门的作用是改变使能端的电平，减少使能端.先列出它的功能表如下表所示:
逻辑电路图如图(3)所示:
（2）多路分配器它的功能是把输入数据分配给不同的通道上，相当于一个单刀多掷开关。
A0
A1
A2
D
F
0 0 0
D0----D7
D0
0 0 1
D0----D7
D1
0 1 0
D0----D7
D2
0 1 1
D0----D7
D3
1 0 0
D0----D7
D4
1 0 1
D0----D7
D5
1 1 0
D0----D7
D6
1 1 1
D0----D7
D7