1.最小项的基本概念
由A、B、C三个逻辑变量构成的许多乘积项中有八个被称为A、B、C的最小项的乘积项,它们的特点是
1.每项都只有三个因子
2.每个变量都是它的一个因子
3.每一变量或以原变量(A、B、C)的形式出现,或以反(非)变量(A、B、C)的形式出现,各出现一次
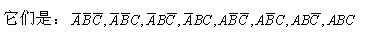
一般情况下,对n个变量来说,最小项共有2n个,如n=3时,最小项有23=8个
2.最小项的性质
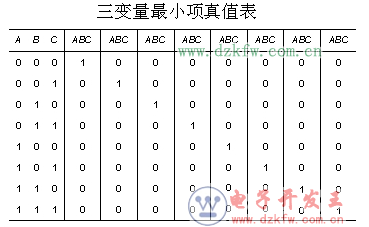
为了分析最小项的性质,以下列出3个变量的所有最小项的真值表。
由此可见,最小项具有下列性质:
(1)对于任意一个最小项,只有一组变量取值使得它的值为1,而在变量取其他各组值时,这个最小项的值都是0。
(2)不同的最小项,使它的值为1的那一组变量取值也不同。
(3)对于变量的任一组取值,任意两个最小项的乘积为0。
(4)对于变量的任一组取值,全体最小项之和为1。
3.最小项的编号
最小项通常用mi表示,下标i即最小项编号,用十进制数表示。以ABC为例,因为它和011相对应,所以就称ABC是和变量取值011相对应的最小项,而011相当于十进制中的3,所以把ABC记为m3按此原则,3个变量的最小项

二、逻辑函数的最小项表达式


三、用卡诺图表示逻辑函数
1.卡诺图的引出
一个逻辑函数的卡诺图就是将此函数的最小项表达式中的各最小项相应地填入一个特定的方格图内,此方格图称为卡诺图。
卡诺图是逻辑函数的一种图形表示。
下面从讨论一变量卡诺图开始,逐步过渡到多变量卡诺图。
大家知道,n个变量的逻辑函数有2n个最小项,因此一个变量的逻辑函数有两个最小项。
比如有一个变量D,其逻辑函数L的最小项表达式为:


综上所述,可归纳“折叠展开”的法则如下:
①新增加的方格按展开方向应标以新变量。
②新的方格内最小项编号应为展开前对应方格编号加2n-1。
按照同样的方法,可从折叠的2变量卡诺图展开获得3变量卡诺图。3变量逻辑函数L(B,C,D)应有8个最小项,可用8个相邻的方格来表示。新增加的4个方格按展开方向应标以新增加的变量B(以区别于原来的变量C、D)。而且,新增加的方格内最小项的编号为展开前对应方格编号加2n-1=23-1=4,这样即可获得3变量卡诺图如下:

在使用时,只要熟悉了卡诺图上各变量的取值情况(即方格外各变量A、B、C、D等取值的区域),就可直接填入对应的最小项。
将上图中的数码编号与最小项的编号——对应,可以得到下面这种形式的卡诺图。
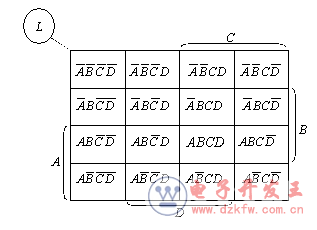
2.卡诺图的特点
上面所得各种变量的卡诺图,其共同特点是可以直接观察相邻项
。也就是说,各小方格对应于各变量不同的组合,而且上下左右在几何上相邻的方格内只有一个因子有差别,这个重要特点成为卡诺图化简逻辑函数的主要依据。在卡诺图水平方向的同一行里,最左和最右端的方格也是符合上述相邻规律的,例如,m4和m6的差别仅在C和。同样,垂直方向同一列里最上端和最下端两个方格也是相邻的,这是因为都只有一个因子有差别。这个特点说明卡诺图呈现循环邻接的特性。
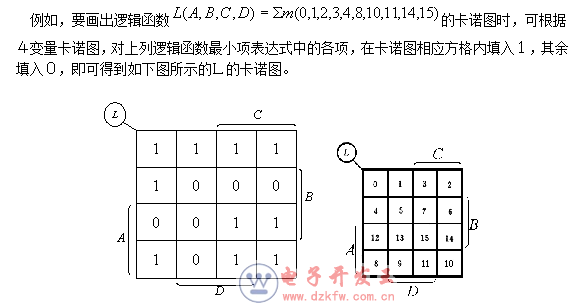
3.已知逻辑函数画卡诺图
根据逻辑函数的最小项表达式和卡诺图的一般形式,就可以得到相应的卡诺图。