在本教程中,我们将研究使用中坐标规则和分析规则计算正弦波形的“平均”或平均电压值
用于查找交替波形的平均电压与发现其RMS值的非常相似,此时的差异是瞬时值不是平方的,我们没有找到求和平均值的平方根。
无论是正弦波,方波还是三角波,周期波形的平均电压(或电流)定义为:“波形下面积相对于时间的商”。换句话说,沿时间轴对所有瞬时值进行平均,时间为一个完整周期( T )。
对于周期波形,水平轴上方的区域水平轴下方的区域为负值,为正值。结果是对称交替量的平均值或平均值因此为零,(0)因为水平轴上方的区域(正半周期)与轴下方的区域(负半周期)相同,并且从而相互抵消。这是因为当我们对两个区域进行数学运算时,负区域会抵消产生零平均电压的正区域。
然后是对称交替量的平均值或平均值,例如正弦波,是我们刚才所说的,仅在一个周期的一半测量的平均值,无论峰值幅度如何,一个完整周期的平均值都为零。
电气术语平均值电压和平均电压或甚至平均电流可用于AC和DC电路分析或计算。用于表示平均值的符号定义为: V AV 或 I AV 。
平均电压图形方法
再次考虑前一个RMS电压教程的正半周期。通过采用等间隔的瞬时值,可以以合理的精度再次找到波形的平均电压或平均电压。
波形的正半部分被分成任意数量的“n”等分或者mid-ordinates 。因此,每个中坐标的宽度将 n o 度(或 t 秒),并且每个中坐标的高度将相等沿波形x轴的那个点的波形的瞬时值。
图形方法
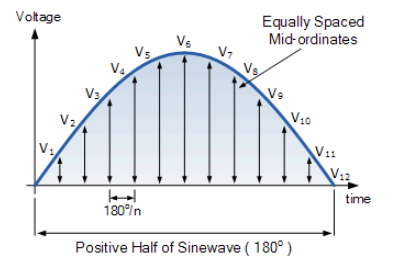
电压波形的每个中间值都加到下一个和总和, V 1 到 V 12 除以用于给出“平均电压”的中间数。然后平均电压( V AV )是电压波形的中间坐标的平均值,并给出如下:

并且对于上面的简单示例,平均电压因此计算如下:
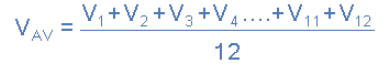
如前所述,我们再假设一个20伏峰值的交流电压在一个半周期内变化如下:

平均电压因此计算的值为:
然后使用图形方法的半个周期的平均电压值为: 12.64伏。
平均电压分析方法
如前所述,两个半部完全相似的周期性波形的平均电压,无论是正弦波还是非正弦波,在一个完整周期内将为零。然后,通过仅在一个半周期上加上电压的瞬时值来获得平均值。但是在非对称或复杂波的情况下,平均电压(或电流)必须在整个周期循环中进行数学处理。
平均值可以通过采用近似的数学方法得到。曲线下面的区域以不同的间隔到底座的距离或长度,这可以使用三角形或矩形来完成,如图所示。
区域的近似

通过近似曲线下方矩形的区域,我们可以粗略地了解每个区域的实际区域。通过将所有这些区域加在一起,可以找到平均值。如果使用无限数量的较小的较薄矩形,则当它接近 2 /π时,最终结果将更准确。
曲线下面积可以通过各种方式找到近似方法,如梯形法则,中段规则或 Simpson规则。然后是周期波正半周期下的数学区域,定义为 V (t) = Vp.cos(ωt),周期为 T 使用积分如下:

其中:0和π是整合的限制因素我们正在确定半个周期内电压的平均值。然后曲线下面的区域最终给出为 Area = 2V P 。由于我们现在知道正半周期(或负半周期)下的面积,我们可以通过积分半个周期的正弦量并除以周期的一半来轻松确定正弦波形的正(或负)区域的平均值。 。
例如,如果正弦波的瞬时电压给定为: v =Vp.sinθ,则正弦波的周期为:2π,然后:

因此,它作为正弦波平均电压的标准公式给出as:
平均电压公式
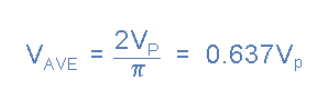
平均电压( V AV )通过将峰值电压值乘以常数0.637来确定正弦波形,其是2除以pi(π)。平均电压(也可称为平均值)取决于波形的大小,而不是频率或相位角的函数。
因此,这个平均值或平均值(正弦波形的电压或电流也可以显示为面积和时间的等效DC值。
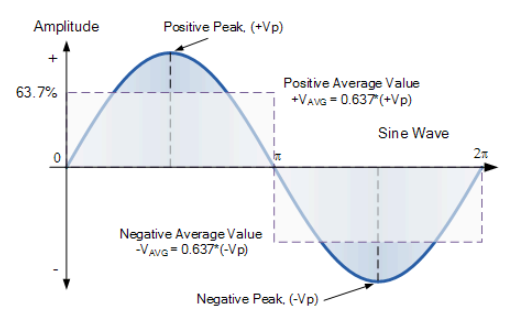
在一个完整周期内平均值为零,因为正平均面积将被负平均面积(V AVG - ( - V AVG ))取消。这两个区域的总和,因此在正弦波的一个完整周期内产生零平均电压。
参考上面的图形示例,峰值电压,( V pk )为20伏特。因此,使用分析方法,平均电压计算如下:
V AV = V pk x0.637 = 20x0.637 = 12.74伏
这是一样的图形方法的值。
要从给定的平均电压值中找到峰值,只需重新排列公式并除以常数。例如,如果平均值为65伏,那么正弦峰值V pk 是什么。
V pk = V AV &pide;0.637 = 65&pide;0.637 = 102伏
请注意,将峰值或最大值乘以常数0.637ONLY适用于正弦波形。
平均电压汇总
然后总结一下。当处理交流电压(或电流)时,术语平均值通常采用一个完整周期,而术语平均值用于周期周期的一半。
一个完整周期内整个正弦波形的平均值为零,因为两个半部相互抵消,所以平均值取半个周期。电压或电流的正弦波的平均值是峰值的0.637倍( Vp 或 Ip 。这些平均值之间的数学关系适用于交流电流和交流电压。
有时需要能够计算整流器或脉冲型电路(如PWM电机电路)的直流电压或电流输出值,因为电压或电流虽然没有反转由于没有相位反转,因此使用平均值并且RMS(均方根)值对于此类应用而言并不重要。
之间的主要区别RMS电压和平均电压,是周期波的平均值是在波形的给定周期内在曲线下所取的所有瞬时面积的平均值,并且在在一个正弦量的情况下,这个周期被视为波的周期的一半。为方便起见,正半周通常使用循环。
波形的有效值或均方根(RMS)值是波的有效热值与稳定的DC值相比较是一个完整周期内瞬时值的平方平均值的平方根。
仅对于纯正弦波形,可以很容易地计算出平均电压和RMS电压(或电流) as:
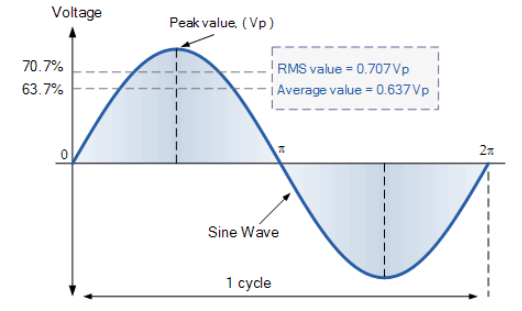
平均值 = 0.637×最大值或峰值,Vpk
RMS值 = 0.707×最大值或峰值,Vpk
关于使用平均电压和RMS的最后评论电压的。两个值都可用于表示正弦交替波形的“形状因子”。形状因子定义为AC波形的形状,是RMS电压除以平均电压(形状因子= rms值/平均值)。
所以对于a正弦波或复杂波形的形状因子如下:( π/(2√ 2 )),它近似等于常数,1.11。形状因子是比率,因此没有电气单位。如果已知正弦波形的形状因子,则可以使用RMS电压值找到平均电压,反之亦然,因为平均电压是正弦波的RMS电压值的0.9倍。
