如前所述,频率特性法是一种工程方法,主要采用的是一种图解法。常用的频率特性图示方法分两种:极坐标图示法、对数坐标图示法。本节介绍极坐标图示法。
由于频率特性![]() 是一个复数,因而可在复平面上用直角坐标形式表示:
是一个复数,因而可在复平面上用直角坐标形式表示:
![]() (5-21)
(5-21)
同样也可用极坐标形式写成:
![]() (5-22)
(5-22)
式中,![]() 。这样,
。这样,![]() 可用幅值为
可用幅值为![]() 、相角为
、相角为![]() 的向量来表示。当输入信号的频率ω由
的向量来表示。当输入信号的频率ω由![]() 变化时,向量
变化时,向量![]() 的幅值和相位也随之作相应的变化,其端点在复平面上移动而形成的轨迹曲线,称为极坐标图,又称为
的幅值和相位也随之作相应的变化,其端点在复平面上移动而形成的轨迹曲线,称为极坐标图,又称为![]() 的幅相特性或奈奎斯特(Nyquist)曲线,简称奈氏图。
的幅相特性或奈奎斯特(Nyquist)曲线,简称奈氏图。
5.2.1 典型环节的奈氏曲线
为了便于对频率特性作图,本章中的开环传递函数均以时间常数形式表示。具有这种形式的开环频率特性 一般由下列五种典型环节组成。
1)比例环节K;
2)一阶环节![]() ;
;
3)积分和微分环节![]() ;
;
4)二阶环节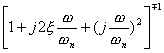 ;
;
5)延迟环节![]() 。
。
1.比例环节
比例环节的频率特性为
![]() (5-23)
(5-23)
由于K是一个与ω无关的常数,它的相角为零度,因而它的奈氏图为![]() 复平面实轴上的一个定点,如图5-5所示。
复平面实轴上的一个定点,如图5-5所示。
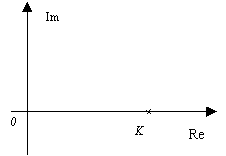 图5-5 比例环节频率特性极坐标图
图5-5 比例环节频率特性极坐标图
2.积分和微分环节
积分环节的频率特性为
![]() (5-24)
(5-24)
由上式可见,积分环节的幅值与ω成反比,相角恒为![]() ,其奈氏图如图5-6a所示。显然积分环节是一个相位滞后环节,每当信号经过一个积分环节后,其相位滞后
,其奈氏图如图5-6a所示。显然积分环节是一个相位滞后环节,每当信号经过一个积分环节后,其相位滞后![]() 。
。
对于微分环节,其频率特性为
![]() (5-25)
(5-25)
它的奈氏图应如图5-6b所示。由图可见,微分环节是一个相位超前环节,每当系统增加一个微分环节,将使相位增加![]() 。
。
比较积分环节和微分环节可以发现,它们的幅值特性和相位特性均刚刚相反。
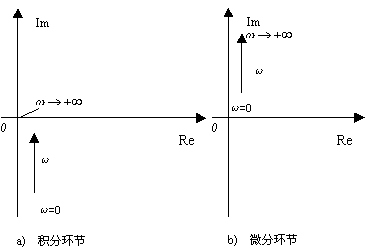 图5-6 积分、微分环节频率特性极坐标图
图5-6 积分、微分环节频率特性极坐标图
3.一阶惯性环节
一阶惯性环节的频率特性为
![]() (5-26)
(5-26)
式中,![]()
若将上式写成实频特性和虚频特性的形式:
![]()
式中
![]() ,
,![]()
于是得
![]()
也即
![]()
显然上式是一个圆的方程,其圆心为![]() ,半径为
,半径为![]() ,如图5-7a所示。可见,一阶惯性环节是一个相位滞后环节,其最大滞后角为
,如图5-7a所示。可见,一阶惯性环节是一个相位滞后环节,其最大滞后角为![]() ,此时频率为无穷大。
,此时频率为无穷大。
一阶微分环节的频率特性为
![]() (5-27)
(5-27)
式中![]() 。当
。当![]() 时,其幅值从
时,其幅值从![]() ,相角
,相角![]() ,因此它是一个相位超前环节。图5-7b为它的奈氏图。
,因此它是一个相位超前环节。图5-7b为它的奈氏图。
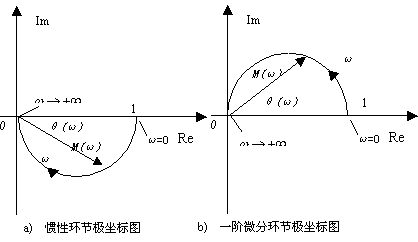 图5-7 比例环节频率特性极坐标图
图5-7 比例环节频率特性极坐标图
4.二阶振荡环节和二阶微分环节
根据第三章内容,典型二阶振荡环节的频率特性可写为
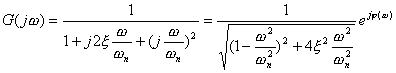 (5-28)
(5-28)
式中
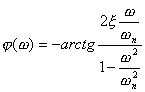 (5-29)
(5-29)
由式(5-28)可知,振荡环节奈氏图的低频段和高频段分别为
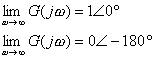
当![]() 时,
时,![]() ,其相角为
,其相角为![]() 。
。
当ξ值已知,则由式(5-28)可求得对应于不同ω值时的![]() 和
和![]() 值。图5-8为式(5-28)在不同ξ值下用Matlab绘制的奈氏曲线。当
值。图5-8为式(5-28)在不同ξ值下用Matlab绘制的奈氏曲线。当![]() 时,在奈氏曲线上距原点最远的点所对应的频率就是振荡环节的谐振频率
时,在奈氏曲线上距原点最远的点所对应的频率就是振荡环节的谐振频率![]() ,其谐振峰值
,其谐振峰值![]() 用
用![]() 与
与![]() 之比来表示。
之比来表示。
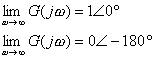 图5-8 二阶振荡环节不同ξ的奈氏曲线
图5-8 二阶振荡环节不同ξ的奈氏曲线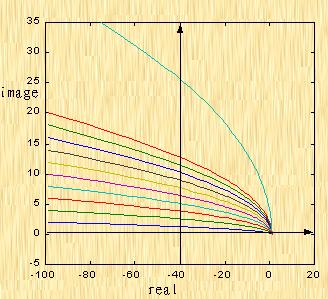 图5-9 二阶微分环节不同ξ的奈氏曲线
图5-9 二阶微分环节不同ξ的奈氏曲线
由第三章的讨论可知,当![]() 时,振荡环节不产生谐振,
时,振荡环节不产生谐振,![]() 向量的长度将随着ω的增加而单调地减小。当
向量的长度将随着ω的增加而单调地减小。当![]() 时,
时,![]() 有两个相异的实数极点。如果ξ值足够大,则其中一个极点靠近s平面的坐标原点,另一个极点远离虚轴。显然,远离虚轴的这个极点对瞬态响应的影响很小,此时式(5-28)的特性与一阶惯性环节相类同,它的奈氏图近似于一个半圆。
有两个相异的实数极点。如果ξ值足够大,则其中一个极点靠近s平面的坐标原点,另一个极点远离虚轴。显然,远离虚轴的这个极点对瞬态响应的影响很小,此时式(5-28)的特性与一阶惯性环节相类同,它的奈氏图近似于一个半圆。
二阶微分环节的频率特性为
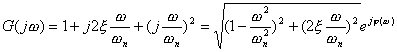 (5-30)
(5-30)
式中
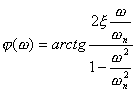
图5-9为二阶微分环节的奈氏图。
5.时滞环节
时滞环节的频率特性为
![]() (5-31)
(5-31)
由于时滞环节的幅频值恒为1,而其相位与ω成比例变化,因而它的奈氏图是一个单位圆,如图5-10所示。在低频区,时滞环节![]() 和惯性环节
和惯性环节![]() 的频率特性很接近,如图5-11所示。因为
的频率特性很接近,如图5-11所示。因为
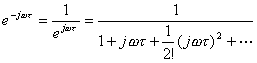
当![]() 时,上式可近似为
时,上式可近似为
![]() (5-32)
(5-32)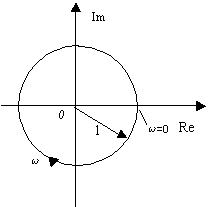 图5-10 时滞环节奈氏图
图5-10 时滞环节奈氏图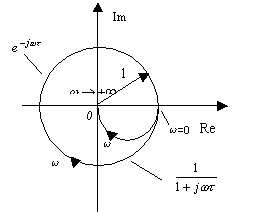 图5-11时滞环节与下一阶惯性环节在低频段的等效性
图5-11时滞环节与下一阶惯性环节在低频段的等效性
因此当![]() 时,时滞环节通常近似地可用惯性环节表示。
时,时滞环节通常近似地可用惯性环节表示。
5.2.2 开环系统的奈奎斯特图
在采用频率特性法对控制系统进行分析时,一般采用两种方法:一种是直接采用开环频率特性分析闭环系统的性能,另外一种是根据开环频率特性曲线绘制闭环频率特性,然后用闭环频率特性分析闭环系统的性能。但不论采用哪一种方法,在用极坐标图进行分析时,首先应作出极坐标形式的开环幅值特性和开环相位特性曲线。
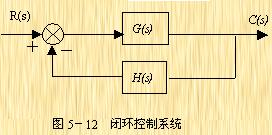
对于如图5-12的闭环控制系统,其开环传递函数为![]() ,把开环频率特性写作如下的极坐标形式或直角坐标形式:
,把开环频率特性写作如下的极坐标形式或直角坐标形式:
![]() (5-33)
(5-33)
当ω由 变化时,逐点计算相应的 和 的值,可画出开环系统的奈氏图。在控制工程中,一般只需画出奈氏曲线的大致形状和几个关键点的位置,如与实轴相交点、与虑轴相交点及曲线的旋转方向等,即可对控制系统进行分析。
例5-2试绘制下列开环传递函数的奈奎斯特曲线:
试绘制下列开环传递函数的奈奎斯特曲线:
![]()
解:该开环系统由三个典型环节串联组成:一个比例环节![]() 、两个一阶惯性环节
、两个一阶惯性环节![]() 和
和![]() 。这三个环节的幅、相频率特性分别为:
。这三个环节的幅、相频率特性分别为:
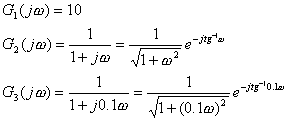
因而开环系统的幅频特性:
![]()
相频特性:
![]()
取不同的频率 值,可得到对应的幅值和相角,根据这些值可绘制出开环系统的奈氏图如图5-13。
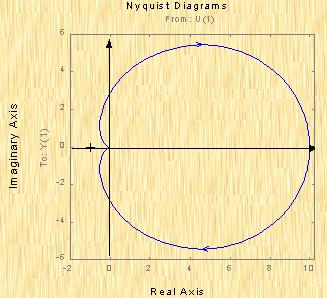 图5-13 开环系统的奈氏图
图5-13 开环系统的奈氏图
事实上,在Matlab中,有专门的函数用于绘制开环系统的极坐标图:Nyquist。关于该命令的详细说明,可见第九章说明。对于本题,可用如下命令:
g=tf(10,conv([1,1],[0.1,1]))
Transfer funcTIon:
10
-------------------
0.1 s^2 + 1.1 s + 1
nyquist(g)
在实际的控制系统中,开环传递函数常常由若干典型环节串联而成,因此通过对典型系统的奈氏图的绘制将有助于用奈氏图分析和设计控制系统。下面通过对不同类型系统的奈氏图在 和 时特征的分析,简要研究控制系统的静态和动态性能。
1.0型系统
设0型系统的开环频率特性为
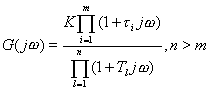 (5-34)
(5-34)
当![]() 时,
时,![]() 、
、![]() ,即为实轴上的一点(K,0),它是0型系统奈氏图的始点。当
,即为实轴上的一点(K,0),它是0型系统奈氏图的始点。当![]() 时,
时,![]() 、
、![]() 。当
。当![]() 时,奈氏曲线的具体形状由开环传递函数所含的具体环节和参数所确定。
时,奈氏曲线的具体形状由开环传递函数所含的具体环节和参数所确定。
2.I型系统
设I型系统的开环频率特性为
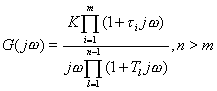 (5-35)
(5-35)
由上式不难看出,当![]() 时,
时,![]()
![]() ;当
;当![]() 时,
时,![]()
![]() 。
。
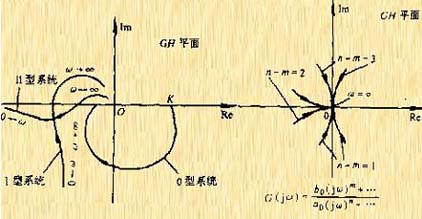 图5-14a 0型、1型和II型系统的奈氏图
图5-14a 0型、1型和II型系统的奈氏图
图5-14b 开环系统高频段的奈氏图
3、Ⅱ型系统
设Ⅱ型系统的开环频率特性为
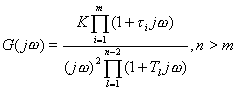 (5-36)
(5-36)
由式(5-36)可知,当![]() 时,
时,![]()
![]() ;当
;当![]() 时,
时,![]()
![]() 。
。
综上所述,开环系统极坐标图的低频部分是由因式![]() 确定的。对于0型系统,
确定的。对于0型系统,![]()
![]() ;而对于I型和I型以上的
;而对于I型和I型以上的![]() 型系统,
型系统,
![]()
![]() 。如果
。如果![]() ,当
,当![]() 时,
时,![]() ,
,![]() 曲线以顺时针方向按
曲线以顺时针方向按![]() 的角度趋向于坐标原点,如果(n-m)是偶数,则曲线与横轴相切;反之,若是奇数,则曲线与虚轴相切。图5-14a为0型、I型和Ⅱ型系统的奈氏图。图5-14b为高频段的奈氏图。
的角度趋向于坐标原点,如果(n-m)是偶数,则曲线与横轴相切;反之,若是奇数,则曲线与虚轴相切。图5-14a为0型、I型和Ⅱ型系统的奈氏图。图5-14b为高频段的奈氏图。
例5-3已知0型系统、I型系统和II型系统的开环传递函数分别为....
已知0型系统、I型系统和II型系统的开环传递函数分别为
![]()
![]()
![]()
试绘制它们对应的奈氏图。
解(1)0型系统的频率特性为
![]() 式中,
式中,![]() ,
,
分别取 ,由上述两式,计算不同ω值时的 和 。据此,可得到图5-15所示的奈氏图。根据第三章劳斯判据可知,当 ,闭环系统稳定,表现在奈氏图上是极坐标图不包围(-1,j0),这与后面将介绍的奈氏稳定判据是一致的。
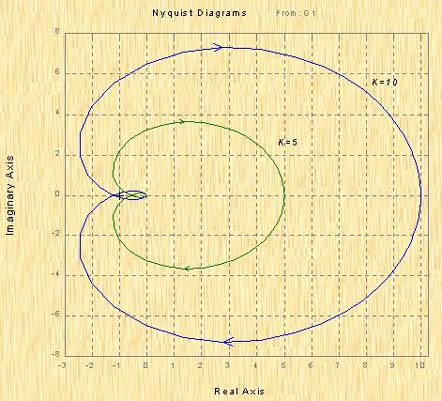 图5-15 K=5、10时的奈氏图
图5-15 K=5、10时的奈氏图
(2)I型系统的频率特性为
![]() 其中
其中![]() ,
,
把上式改写为
![]()
上式中,当![]() 时,
时,![]() ,即
,即![]()
![]() ;当
;当![]() 时,
时,![]()
![]() 。据此画出图5-16所示的奈氏图。
。据此画出图5-16所示的奈氏图。
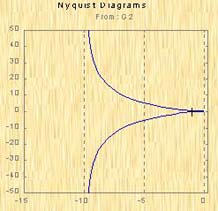 图5-16 I型系统的奈氏图
图5-16 I型系统的奈氏图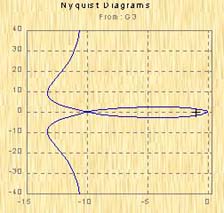 图5-17 II型系统的奈氏图
图5-17 II型系统的奈氏图
(3)该Ⅱ型系统的开环频率特性为
![]() 式中,
式中,![]() ,
,
据此画出图5-17所示的奈氏图。
由于采用了Matlab,对于I、II型系统,在无穷远处的极坐标无法在图中标明,但从图中同样可以看到,当频率接近零时,极坐标曲线渐近于平行于虚轴的-10,这一点可将幅值频率特性写成实频、虚频形式得到验证。如前所述,频率特性法是一种工程方法,主要采用的是一种图解法。常用的频率特性图示方法分两种:极坐标图示法、对数坐标图示法。本节介绍极坐标图示法。
由于频率特性![]() 是一个复数,因而可在复平面上用直角坐标形式表示:
是一个复数,因而可在复平面上用直角坐标形式表示:
![]() (5-21)
(5-21)
同样也可用极坐标形式写成:
![]() (5-22)
(5-22)
式中,![]() 。这样,
。这样,![]() 可用幅值为
可用幅值为![]() 、相角为
、相角为![]() 的向量来表示。当输入信号的频率ω由
的向量来表示。当输入信号的频率ω由![]() 变化时,向量
变化时,向量![]() 的幅值和相位也随之作相应的变化,其端点在复平面上移动而形成的轨迹曲线,称为极坐标图,又称为
的幅值和相位也随之作相应的变化,其端点在复平面上移动而形成的轨迹曲线,称为极坐标图,又称为![]() 的幅相特性或奈奎斯特(Nyquist)曲线,简称奈氏图。
的幅相特性或奈奎斯特(Nyquist)曲线,简称奈氏图。
5.2.1 典型环节的奈氏曲线
为了便于对频率特性作图,本章中的开环传递函数均以时间常数形式表示。具有这种形式的开环频率特性 一般由下列五种典型环节组成。
1)比例环节K;
2)一阶环节![]() ;
;
3)积分和微分环节![]() ;
;
4)二阶环节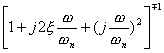 ;
;
5)延迟环节![]() 。
。
1.比例环节
比例环节的频率特性为
![]() (5-23)
(5-23)
由于K是一个与ω无关的常数,它的相角为零度,因而它的奈氏图为![]() 复平面实轴上的一个定点,如图5-5所示。
复平面实轴上的一个定点,如图5-5所示。
 图5-5 比例环节频率特性极坐标图
图5-5 比例环节频率特性极坐标图
2.积分和微分环节
积分环节的频率特性为
![]() (5-24)
(5-24)
由上式可见,积分环节的幅值与ω成反比,相角恒为![]() ,其奈氏图如图5-6a所示。显然积分环节是一个相位滞后环节,每当信号经过一个积分环节后,其相位滞后
,其奈氏图如图5-6a所示。显然积分环节是一个相位滞后环节,每当信号经过一个积分环节后,其相位滞后![]() 。
。
对于微分环节,其频率特性为
![]() (5-25)
(5-25)
它的奈氏图应如图5-6b所示。由图可见,微分环节是一个相位超前环节,每当系统增加一个微分环节,将使相位增加![]() 。
。
比较积分环节和微分环节可以发现,它们的幅值特性和相位特性均刚刚相反。
 图5-6 积分、微分环节频率特性极坐标图
图5-6 积分、微分环节频率特性极坐标图
3.一阶惯性环节
一阶惯性环节的频率特性为
![]() (5-26)
(5-26)
式中,![]()
若将上式写成实频特性和虚频特性的形式:
![]()
式中
![]() ,
,![]()
于是得
![]()
也即
![]()
显然上式是一个圆的方程,其圆心为![]() ,半径为
,半径为![]() ,如图5-7a所示。可见,一阶惯性环节是一个相位滞后环节,其最大滞后角为
,如图5-7a所示。可见,一阶惯性环节是一个相位滞后环节,其最大滞后角为![]() ,此时频率为无穷大。
,此时频率为无穷大。
一阶微分环节的频率特性为
![]() (5-27)
(5-27)
式中![]() 。当
。当![]() 时,其幅值从
时,其幅值从![]() ,相角
,相角![]() ,因此它是一个相位超前环节。图5-7b为它的奈氏图。
,因此它是一个相位超前环节。图5-7b为它的奈氏图。
 图5-7 比例环节频率特性极坐标图
图5-7 比例环节频率特性极坐标图
4.二阶振荡环节和二阶微分环节
根据第三章内容,典型二阶振荡环节的频率特性可写为
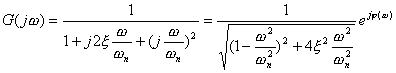 (5-28)
(5-28)
式中
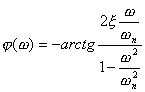 (5-29)
(5-29)
由式(5-28)可知,振荡环节奈氏图的低频段和高频段分别为
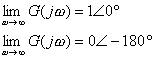
当![]() 时,
时,![]() ,其相角为
,其相角为![]() 。
。
当ξ值已知,则由式(5-28)可求得对应于不同ω值时的![]() 和
和![]() 值。图5-8为式(5-28)在不同ξ值下用Matlab绘制的奈氏曲线。当
值。图5-8为式(5-28)在不同ξ值下用Matlab绘制的奈氏曲线。当![]() 时,在奈氏曲线上距原点最远的点所对应的频率就是振荡环节的谐振频率
时,在奈氏曲线上距原点最远的点所对应的频率就是振荡环节的谐振频率![]() ,其谐振峰值
,其谐振峰值![]() 用
用![]() 与
与![]() 之比来表示。
之比来表示。
 图5-8 二阶振荡环节不同ξ的奈氏曲线
图5-8 二阶振荡环节不同ξ的奈氏曲线 图5-9 二阶微分环节不同ξ的奈氏曲线
图5-9 二阶微分环节不同ξ的奈氏曲线
由第三章的讨论可知,当![]() 时,振荡环节不产生谐振,
时,振荡环节不产生谐振,![]() 向量的长度将随着ω的增加而单调地减小。当
向量的长度将随着ω的增加而单调地减小。当![]() 时,
时,![]() 有两个相异的实数极点。如果ξ值足够大,则其中一个极点靠近s平面的坐标原点,另一个极点远离虚轴。显然,远离虚轴的这个极点对瞬态响应的影响很小,此时式(5-28)的特性与一阶惯性环节相类同,它的奈氏图近似于一个半圆。
有两个相异的实数极点。如果ξ值足够大,则其中一个极点靠近s平面的坐标原点,另一个极点远离虚轴。显然,远离虚轴的这个极点对瞬态响应的影响很小,此时式(5-28)的特性与一阶惯性环节相类同,它的奈氏图近似于一个半圆。
二阶微分环节的频率特性为
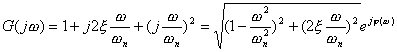 (5-30)
(5-30)
式中
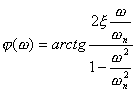
图5-9为二阶微分环节的奈氏图。
5.时滞环节
时滞环节的频率特性为
![]() (5-31)
(5-31)
由于时滞环节的幅频值恒为1,而其相位与ω成比例变化,因而它的奈氏图是一个单位圆,如图5-10所示。在低频区,时滞环节![]() 和惯性环节
和惯性环节![]() 的频率特性很接近,如图5-11所示。因为
的频率特性很接近,如图5-11所示。因为
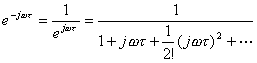
当![]() 时,上式可近似为
时,上式可近似为
![]() (5-32)
(5-32) 图5-10 时滞环节奈氏图
图5-10 时滞环节奈氏图 图5-11时滞环节与下一阶惯性环节在低频段的等效性
图5-11时滞环节与下一阶惯性环节在低频段的等效性
因此当![]() 时,时滞环节通常近似地可用惯性环节表示。
时,时滞环节通常近似地可用惯性环节表示。
5.2.2 开环系统的奈奎斯特图
在采用频率特性法对控制系统进行分析时,一般采用两种方法:一种是直接采用开环频率特性分析闭环系统的性能,另外一种是根据开环频率特性曲线绘制闭环频率特性,然后用闭环频率特性分析闭环系统的性能。但不论采用哪一种方法,在用极坐标图进行分析时,首先应作出极坐标形式的开环幅值特性和开环相位特性曲线。

对于如图5-12的闭环控制系统,其开环传递函数为![]() ,把开环频率特性写作如下的极坐标形式或直角坐标形式:
,把开环频率特性写作如下的极坐标形式或直角坐标形式:
![]() (5-33)
(5-33)
当ω由 变化时,逐点计算相应的 和 的值,可画出开环系统的奈氏图。在控制工程中,一般只需画出奈氏曲线的大致形状和几个关键点的位置,如与实轴相交点、与虑轴相交点及曲线的旋转方向等,即可对控制系统进行分析。
例5-2试绘制下列开环传递函数的奈奎斯特曲线:
试绘制下列开环传递函数的奈奎斯特曲线:
![]()
解:该开环系统由三个典型环节串联组成:一个比例环节![]() 、两个一阶惯性环节
、两个一阶惯性环节![]() 和
和![]() 。这三个环节的幅、相频率特性分别为:
。这三个环节的幅、相频率特性分别为:
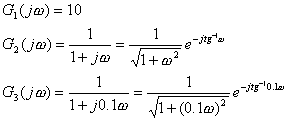
因而开环系统的幅频特性:
![]()
相频特性:
![]()
取不同的频率 值,可得到对应的幅值和相角,根据这些值可绘制出开环系统的奈氏图如图5-13。
 图5-13 开环系统的奈氏图
图5-13 开环系统的奈氏图
事实上,在Matlab中,有专门的函数用于绘制开环系统的极坐标图:Nyquist。关于该命令的详细说明,可见第九章说明。对于本题,可用如下命令:
g=tf(10,conv([1,1],[0.1,1]))
Transfer funcTIon:
10
-------------------
0.1 s^2 + 1.1 s + 1
nyquist(g)
在实际的控制系统中,开环传递函数常常由若干典型环节串联而成,因此通过对典型系统的奈氏图的绘制将有助于用奈氏图分析和设计控制系统。下面通过对不同类型系统的奈氏图在 和 时特征的分析,简要研究控制系统的静态和动态性能。
1.0型系统
设0型系统的开环频率特性为
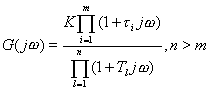 (5-34)
(5-34)
当![]() 时,
时,![]() 、
、![]() ,即为实轴上的一点(K,0),它是0型系统奈氏图的始点。当
,即为实轴上的一点(K,0),它是0型系统奈氏图的始点。当![]() 时,
时,![]() 、
、![]() 。当
。当![]() 时,奈氏曲线的具体形状由开环传递函数所含的具体环节和参数所确定。
时,奈氏曲线的具体形状由开环传递函数所含的具体环节和参数所确定。
2.I型系统
设I型系统的开环频率特性为
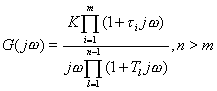 (5-35)
(5-35)
由上式不难看出,当![]() 时,
时,![]()
![]() ;当
;当![]() 时,
时,![]()
![]() 。
。
 图5-14a 0型、1型和II型系统的奈氏图
图5-14a 0型、1型和II型系统的奈氏图
图5-14b 开环系统高频段的奈氏图
3、Ⅱ型系统
设Ⅱ型系统的开环频率特性为
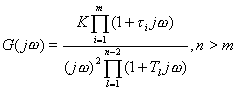 (5-36)
(5-36)
由式(5-36)可知,当![]() 时,
时,![]()
![]() ;当
;当![]() 时,
时,![]()
![]() 。
。
综上所述,开环系统极坐标图的低频部分是由因式![]() 确定的。对于0型系统,
确定的。对于0型系统,![]()
![]() ;而对于I型和I型以上的
;而对于I型和I型以上的![]() 型系统,
型系统,
![]()
![]() 。如果
。如果![]() ,当
,当![]() 时,
时,![]() ,
,![]() 曲线以顺时针方向按
曲线以顺时针方向按![]() 的角度趋向于坐标原点,如果(n-m)是偶数,则曲线与横轴相切;反之,若是奇数,则曲线与虚轴相切。图5-14a为0型、I型和Ⅱ型系统的奈氏图。图5-14b为高频段的奈氏图。
的角度趋向于坐标原点,如果(n-m)是偶数,则曲线与横轴相切;反之,若是奇数,则曲线与虚轴相切。图5-14a为0型、I型和Ⅱ型系统的奈氏图。图5-14b为高频段的奈氏图。
例5-3已知0型系统、I型系统和II型系统的开环传递函数分别为....
已知0型系统、I型系统和II型系统的开环传递函数分别为
![]()
![]()
![]()
试绘制它们对应的奈氏图。
解(1)0型系统的频率特性为
![]() 式中,
式中,![]() ,
,
分别取 ,由上述两式,计算不同ω值时的 和 。据此,可得到图5-15所示的奈氏图。根据第三章劳斯判据可知,当 ,闭环系统稳定,表现在奈氏图上是极坐标图不包围(-1,j0),这与后面将介绍的奈氏稳定判据是一致的。
 图5-15 K=5、10时的奈氏图
图5-15 K=5、10时的奈氏图
(2)I型系统的频率特性为
![]() 其中
其中![]() ,
,
把上式改写为
![]()
上式中,当![]() 时,
时,![]() ,即
,即![]()
![]() ;当
;当![]() 时,
时,![]()
![]() 。据此画出图5-16所示的奈氏图。
。据此画出图5-16所示的奈氏图。
