1 引言
盲源分离可以在对信源知之甚少的情况下，分离出想要的信号。它已成功地应用于生物医学信号处理(如心电图、肌电图、脑电图及脑磁图等)、语音增强、图像增强、数字通信中同频干扰抑制、机械故障检测、雷达信号处理等方面。
在军事通信对抗中，如何摆脱敌方同频干扰的影响以保证我方通信正常是重要的研究课题。已有文献研究了利用肓源分离将频域重合的信号分离这一问题，如文献[3]采用3天线阵列接收，利用盲源分离实现3路同频PAM信号的分离，文献[4]采用相干解调方式实现了多路BPSK信号的分离。这里研究了数字通信的干扰抑制问题，理论分析和计算机仿真表明采用盲源分离的方法可有效抑制同道干扰。
2 盲源分离的数学模型
盲源分离中的“盲”是指当传输信道的特性未知时，从接收信号的阵列中估计出源信号的波形。当然，在缺乏先验知识的情况下，不可能唯一确定源信号，导致所恢复的信号存在一定的模糊性：排序的模糊性和幅度比例伸缩，但所恢复的信号依然保留源信号的波形信息。在一定程度上，这并不影响对信号的理解和处理。
盲源分离的基本模型：假设有n个信源，通过线性混合后，由n个探测器(传感器)接收，整个系统用矩阵表示为：
式中：S为未知的n个源信号，A为n×n的混合矩阵，n为噪声，X为传感器接收的信号。
一般情况下，假设源信号与观测信号维数相同。在噪声不存在或可忽略不计的情况下，这时盲源分离的模型如下：
盲源分离的目标是在一定准则下，寻找矩阵A的逆矩阵的估值A-1，得到对信源S的估计如下：
如果A-1A=I，则Y=S，实现了对源信号的估计。一般情形下，假设源信号统计独立。因此盲源分离问题有时也称独立变量分析(Independent Component Analysis)。
3 数字通信的同道干扰
数字通信是目前无线通信所采用的主要通信方式，其主要调制方式有幅移键控、相移键控和频移键控。
幅移键控信号表示为：
式中:Am表示M个可能的幅度。
相移键控信号表示为：
相移键控发送的载波有M个可能的相位。频移键控信号表示为：
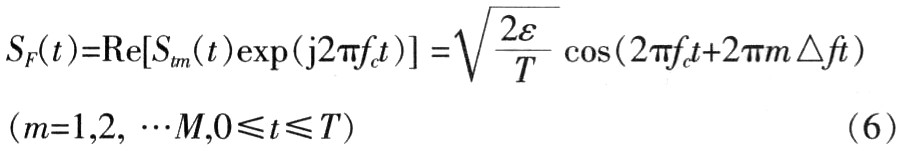
当数字通信的载波频率相同时，通信收发信机之间会产生同道干扰。由于不同发信机之间所发送的信号是独立的，所以可采用盲源分离算法将分离不同发信机所发射的信号。
4 FastICA算法
Hyvarinen等人提出了基于峭度和负熵固定点算法，这一算法具有极快的收敛速度，因此称为：FastICA。FastICA算法属于批处理算法，但其具有相当快的收敛速度，是盲源分离算法中较成功的算法。FastICA算法将非高斯极大化算法和定点迭代相结合，具有三阶收敛速度。衡量非高斯的目标函数有两种：峭度和负熵。因此，FastICA有两种形式：基于峭度最大化和负熵最大化的FastICA算法。下面分别推导基于两种代价函数的FastICA算法。
关于标准峭度的梯度函数：
式中：β是输出信号峭度的符号。
当对混合信号白化后，信号的能量归一化，所以||W||2=1。这样，每次迭代后可将分离向量W归一化。当盲源分离算法到达平衡点时：
由此得到两步迭代快速算法：
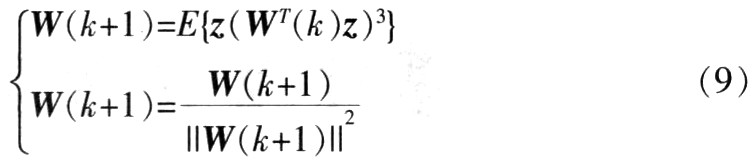总之，基于峭度FastICA总结如下：(1)对观测数据x中心化；(2)白化中心化后的观测数据，得信号z；(3)选择一个正交阵作为初始迭代点；(4)计算W(k+1)=E{z(WT(k)z)3}；(5)将分离向量归一化，即|W(k+1)=W(k+1)/||W(k+1)||2;(6)如果迭代前的分离向量与迭代后的分离向量指向同一方向，即|WT(k+1)W(k)|=1时，终止迭代；(7)提取一个源信号：y(k)=W(k)z。
采用负熵的FastICA具有更稳定的性能，限于篇幅在此不做讨论。FastICA是国际应用较多的一个算法，芬兰赫尔辛基理工大学的网站(http://www．cis．hut．fi／projects／ica)可下载包括：FastICA在内的盲源分离工具包及一些实际采集的数据。
5 计算机仿真
为验证FastICA在分离同频数字通信信号方面的性能，采用计算机仿真方法分别产生BASK和QPSK一组调制信号，其时域波形图如图1a，b所示。随机产生2×2的混合矩阵，分别对以上两个信号进行线性混合，得到混合信号的波形如图1c,d所示。
采用FastICA算法对图1c,d所示的信号进行分离，分离后的信号波形如图1e，f所示。比较图1a，b和图1e，f可以看出分离后信号的波形与发射前信号的波形图基本一致，这说明可以采用FastICA分离同频BASK和QPSK这两种数字通信信号。
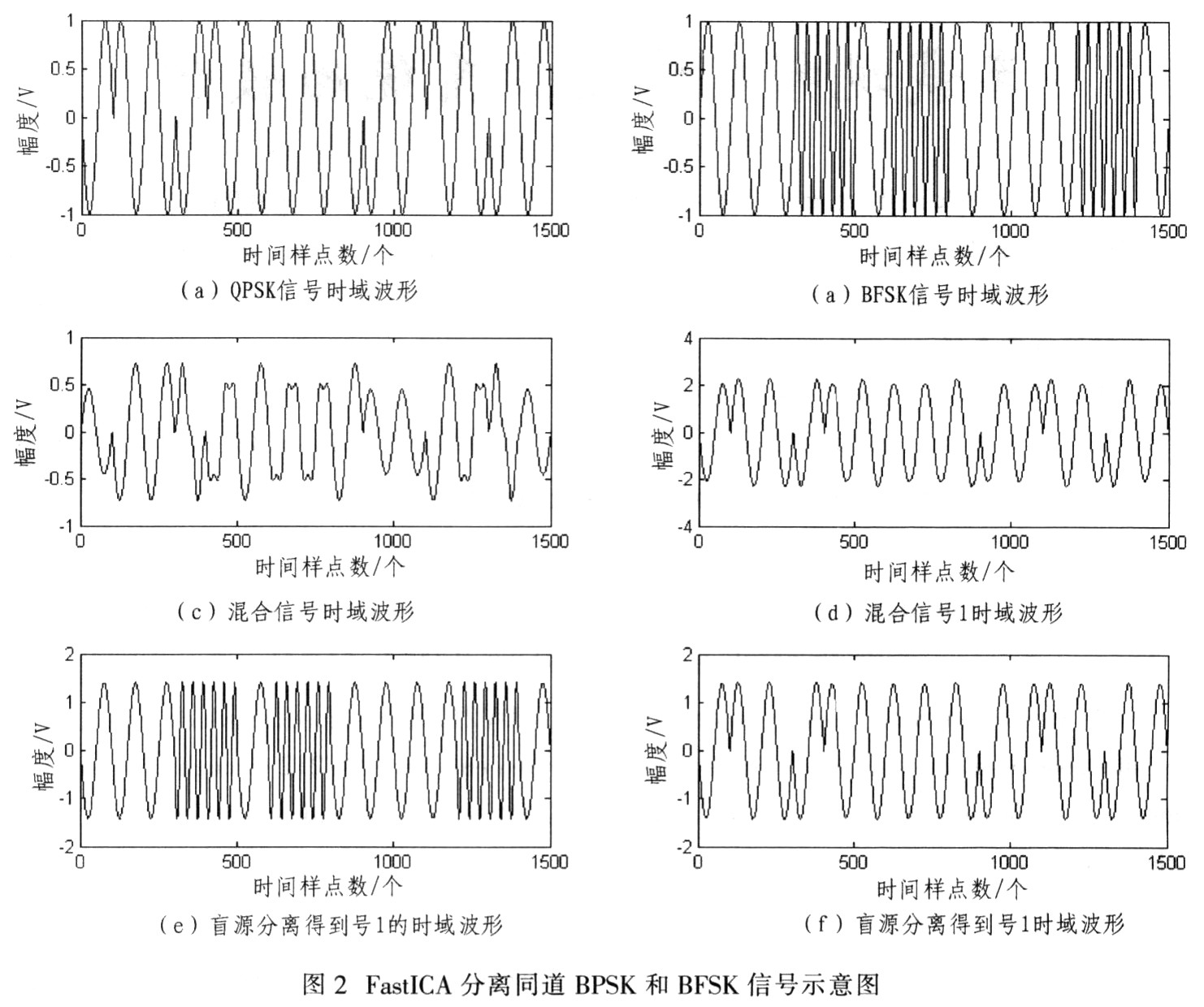
为了检验FastICA在分离其他数字通信信号方面的性能，采用与图1所示类似的过程对频谱重叠的BPSK和BFSK信号进行分离，图2给出了仿真结果。从图2中可看出，FastICA可以分离同道BPSK和BFSK。
6 结论
从仿真试验可看出，FastICA可分离同道BASK和QPSK及。BPSK和BFSK信号的混合，从而达到抑制同频干扰的目的。但对于其他类型数字通信信号的同频干扰问题，FastICA算法是否有效还有待研究。