戴维南定理(Thevenin‘s theorem):含独立电源的线性电阻单口网络N,就端口特性而言,可以等效为一个电压源和电阻串联的单口网络。电压源的电压等于单口网络在负载开路时的电压uoc;电阻R0是单口网络内全部独立电源为零值时所得单口网络N0的等效电阻。
戴维南定理可以在单口外加电流源i,用叠加定理计算端口电压表达式的方法证明如下。在单口网络端口上外加电流源i,根据叠加定理,端口电压可以分为两部分组成。一部分由电流源单独作用(单口内全部独立电源置零)产生的电压u’=Roi,另一部分是外加电流源置零(i=0),即单口网络开路时,由单口网络内部全部独立电源共同作用产生的电压u”=uoc。由此得到:U=u’+u”=Roi + uoc
戴维南等效电路受控源分析
戴维南定理指出,等效二端网络的电动势E等于二端网络开路时的电压,它的串联内阻抗等于网络内部各独立源和电容电压、电感电流都为零时,从这二端看向网络的阻抗Zi。设二端网络N中含有独立电源和线性时不变二端元件(电阻器、电感器、电容器),这些元件之间可以有耦合,即可以有受控源及互感耦合;网络N的两端ɑ、b接有负载阻抗Z(s),但负载与网络N

图2内部诸元件之间没有耦合,U(s)=I(s)/Z(s)(图1)。当网络 N中所有独立电源都不工作(例如将独立电压源用短路代替,独立电流源用开路代替),所有电容电压和电感电流的初始值都为零的时候,可把这二端网络记作N0。这样,负载阻抗Z(s)中的电流I(s)一般就可以按下式1计算(图2)
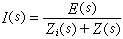
式1式中E(s)是图1二端网络N的开路电压,亦即Z(s)是无穷大时的电压U(s);Zi(s)是二端网络N0呈现的阻抗;s是由单边拉普拉斯变换引进的复变量。和戴维南定理类似,有诺顿定理或亥姆霍兹-诺顿定理。按照这一定理,任何含源线性时不变二端网络均可等效为二端电流源,它的电流J等于在网络二端短路线中流过的电流,并联内阻抗同样等于看向网络的阻抗。这样,图1中的电流I(s)一般可按下式2计算(图3)
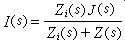
式2式中J(s)是图1二端网络N的短路电流,亦即Z(s)等于零时的电流I(s);Zi(s)及s的意义同前。图2、图3虚线方框中的二端网络,常分别称作二端网络N的戴维南等效电路和诺顿等效电路。
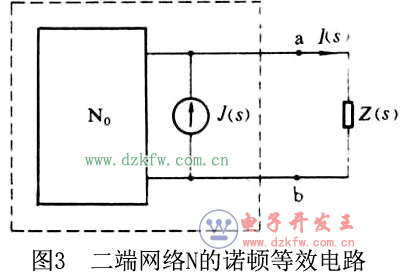
图3在正弦交流稳态条件下,戴维南定理和诺顿定理可表述为:当二端网络N接复阻抗Z时,Z中的电流相量I一般可按以下式3计算
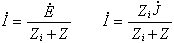
式3式中E、J分别是N的开路电压相量和短路电流相量;Zi是N0呈现的复阻抗;N0是独立电源不工作时的二端网络N。这个定理可推广到含有线性时变元件的二端网络。
