带电粒子在静电场中的有很多种运动模式。常见的场强有：单个带电粒子形成的场强（库仑力），平行板电容器形成的匀强电场，无规则的场强（用电场线来描述的）。本文主要研究的是带电粒子在匀强电场中的类平抛运动模式。
模型基本参量及图像
一质量为m，带电量为q的正粒子从两极板的中部以速度v0水平射入电压为U的竖直向下的匀强电场中。
如图所示，已知极板长度为L，极板间距离为d。存有两种运动模式，一种是粒子能够逃逸出电容，一种则落在电容器的下底板。
基本的物理量描述
（1）初始条件：带电粒子有水平初速度v0；
（2）受力特点：带电粒子受到竖直向下的恒定的电场力F=Eq；加速度
a=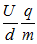
（3）运动特点：水平方向为匀速直线运动，竖直方向为初速度为零的匀加速直线运动。与平抛运动相似，只不过加速度不为g，我们称这样的运动为类平抛运动。
（4）运动时间：若带电粒子与极板不碰撞，在刚逃离电容器时，则运动时间为
；
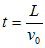若带电粒子与极板碰撞，则运动时间可以从竖直方向求得
，故
几个特殊的物理量
（1）特征描述：侧移（能逃离电容器的y轴偏转量）
（2）能量特点：电场力做正功
。
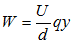电场力做多少正功，粒子动能增加多少，电势能就减少多少。
（3）重要结论：速度偏向角的正切：
，
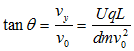位移偏向角的正切：
，
即
，
即带电粒子垂直进入匀强电场，它离开电场时，就好象是从初速度方向的位移中点沿直线射出来的。
例题与结论
如图所示，质量为m电荷量为q的带电粒子以平行于极板的初速度v0射入长L板间距离为d的平行板电容器间，两板间电压为U，求射出时的侧移、偏转角和动能增量．
解：分解为两个独立的分运动：平行极板的匀速运动（运动时间由此分运动决定）
，
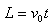垂直极板的匀加速直线运动
,
，
．
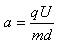偏角：
，
得：
．
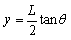穿越电场过程的动能增量是：ΔEK=qEy （注意，一般来说不等于qU），
从例题可以得出结论：
结论一、不同带电粒子从静止进入同一电场加速后再垂直进入同一偏转电场，射出时的偏转角度总和位移偏转量y是相同的，与粒子的q、m无关。
例1．如图所示，电子在电势差为U1的加速电场中由静止开始运动，然后射入电势差为U2的两块平行极板间的电场中，射入方向跟极板平行，整个装置处在真空中，重力可忽略，在满足电子能射出平行板区的条件下，下述四种情况中，一定能使电子的偏转角θ变大的是（ ）
A．U1变大、U2变大B．U1变小、U2变大
C．U1变大、U2变小D．U1变小、U2变小
解析：电子在加速电场中由动能定理得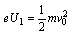
,
电子在偏转电场中有：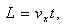
．
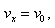
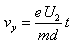由以上各式得：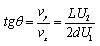
，
可知要使θ增大必然U2变大，U1变小，故选B．答案：B
结论二、粒子垂直进入电场偏转射出后，速度的反向延长线与初速度延长线的交点为粒子水平位移中点。（粒子好像是从中点直线射出！）
例2．证明：在带电的平行金属板电容器中，只要带电粒子垂直电场方向射入（不一定在正中间），且能从电场中射出如图所示，则粒子射入速度v0的方向与射出速度vt的方向的交点O必定在板长L的中点．
证明：粒子从偏转电场中射出时偏距
，
粒子从偏转电场中射出时的偏向角
，
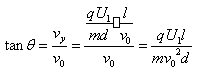作粒子速度的反向延长线，设交于O点，O点与电场边缘的距离为x，则
。
可知，粒子从偏转电场中射出时，就好像是从极板间的
处沿直线射出似的，即证。
结论三、粒子垂直飞入电场偏转射出时，速度偏转角正切值（
）等于位移偏转角正切值（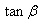
）的两倍（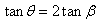
）。
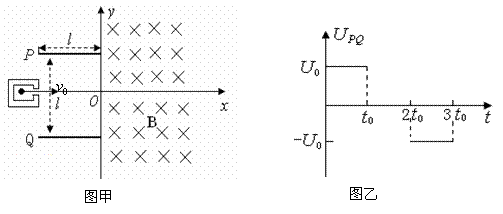
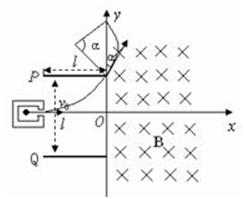
例3．（2009山东）如图甲所示，建立Oxy坐标系，两平行极板P、Q垂直于y轴且关于x轴对称，极板长度和板间距均为l，第一四象限有磁场，方向垂直于Oxy平面向里。位于极板左侧的粒子源沿x轴间右连接发射质量为m、电量为+q、速度相同、重力不计的带电粒子在0～3t时间内两板间加上如图乙所示的电压（不考虑极边缘的影响）。已知t=0时刻进入两板间的带电粒子恰好在t0时，刻经极板边缘射入磁场。上述m、q、l、l0、B为已知量。（不考虑粒子间相互影响及返回板间的情况）
（1）求电压U的大小。
（2）求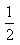
时进入两板间的带电粒子在磁场中做圆周运动的半径。
解析：（1）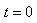
时刻进入两极板的带电粒子在电场中做匀变速曲线运动，
时刻刚好从极板边缘射出，在y轴负方向偏移的距离为
，
则有
,
,
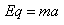联立以上三式，解得两极板间偏转电压为
。
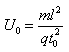（2）
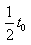时刻进入两极板的带电粒子，前
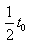时间在电场中偏转，后
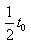时间两极板没有电场，带电粒子做匀速直线运动。带电粒子沿x轴方向的分速度大小为
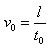,带电粒子离开电场时沿y轴负方向的分速度大小为
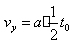,带电粒子离开电场时的速度大小为
,设带电粒子离开电场进入磁场做匀速圆周运动的半径为R，
则有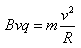
,
联立上式解得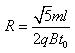
。
本题是高考物理真题，考查的是带电粒子在匀强电场、匀强磁场中的运动。