摘 要：车辆悬架系统作为汽车的一个重要组成部分，其性能好坏会影响到车辆的平顺性与稳定性。以1/4车辆模型为例，从被动悬架到主动悬架，将车辆悬架系统动力学原理与MATLAB仿真软件相结合，即首先利用动力学理论建立其数学模型，然后在仿真软件中建立其相对应的模型进而动态仿真，最后对比结果。实验结果表明，在车轮动载荷大致相同的条件下，设计的主动悬架有效地降低了车体的垂直加速度，与被动悬架相比，优化了约17%，提高了车辆在行驶过程的平顺性和驾驶的稳定性。
0 引言
随着社会经济的发展，人们的生活水平日益提高。越来越多的个人、家庭拥有了属于自己的汽车。乘坐汽车时，人们对于坐车舒适感的要求日渐提高，所以车辆在行驶时的平顺性和操纵的稳定性开始被更多专家所关注。传统意义的汽车悬架系统多为被动悬架系统，其弹簧刚度和减震器阻尼系数是固定而不能改变的，这样的被动悬架系统很难适应人们乘坐汽车舒适性的要求。为使车辆悬架系统在不同路面的激励作用和在不同行驶速度等外在条件的影响下，其操纵稳定性和行驶平顺性受到的影响较小，各种新型悬架系统正在成为研究的热门，出现了一系列的悬架系统的减振控制技术，包括半主动悬架系统和主动悬架系统[1]。
悬架系统包括弹性元件、减振器、导向机构以及横向稳定器等部分。它的主要功能是将车身与车轴由弹性元件连在一起。导向装置的功能是传递系统间的各种力，减震器用来减小车身和轮胎之间摩擦振动能量，保证车辆在行驶过程中的安全，增强乘坐汽车的舒适感。弹性元件用来缓冲外界环境对车体引起的振动，吸收振动的能量[2]。总之，这些机构都是为了使车辆的平顺性达到最佳状态。
在悬架系统的仿真中，普遍采用建立数学模型的方式，所谓的数学模型就是在物理系统和数学方程间设立一套完整的规则，数学模型研究方法比较多样，周期短，成本低。随着现代计算机技术的发展，处理数学模型的手段有了较大突破，可以把若干个参数和运动方程进行互相联系[3-5]。以车辆的1/4模型为例，建立被、主动悬架数学模型，然后进行仿真实验。
1 车辆悬架系统模型
汽车是较复杂的系统，在分析复杂系统时，次要问题可以忽略，将模型进行简化。为便于分析，采用1/4车辆模型，其簧载质量为mv，包括车体、车架及其以上部分的总重。悬架通过减振器和弹簧元件与车轴、轮胎相连接。轮胎和车轴构成的非悬架的质量为ml。
在模型中，考虑人们乘坐汽车的舒适性，即车辆的平顺性，在分析车体质量时，主要考虑垂直、俯仰、侧倾三个自由度。将车辆简化为1/4模型时，车身只具有垂直的自由度，这个自由度的振动对车体的平顺性影响较大，可以将车辆简化成两自由度模型。
此模型中，车胎的阻尼较小，暂且不予考虑，简化后1/4模型如图1、2所示。图中车体的总重为mv，车胎的质量为ml，被动悬架刚度为ks，被动悬架阻尼系数为cs，车胎的刚度为kt，簧载质量位移为xv，非簧载质量位移为xl，路面不平整度的位移为xn，白噪声信号输入为 w（t），主动悬架的制动力为U（t）。
1.1 车辆被动悬架仿真模型的建立
图1所示的被动车辆悬架模型，根据牛顿定律，建立被动悬架系统的运动微分方程，即：
选取状态变量为：xa=xv-xl，xb=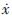
v，xc=xn-xl，xd=
l，组成各个状态的向量为：X=[xa，xb，xc，xd]T，其中，xa为车辆悬架的动扰度，xb为车速，xc车胎动位移，xd为轮速。由式（1）、（2）可得被动悬架系统的状态方程为：
测试车辆悬架性能，主要从该悬架系统对车辆的平顺性和驾驶的稳定性的影响来考虑，主要涉及3个参数：ya=
v=
b，代表车身加速度（ACC）；yb=xv-xl=xa，代表悬架的动扰度（SWS）；yc=xn-xl=xc，代表轮胎动载荷（DTL）。
输出向量U=-KX。由式（1）、（2）得出系统的输出方程为：
Y=CX（5）
其中，
1.2 车辆主动悬架仿真模型的建立
主动悬架与被动悬架的区别在于前者除了具有弹性元件、减振器之外，在车体与车轴之间还安装有制动器，可以调节对汽车的簧载质量和非簧载质量的力，从而加强车辆的平顺性和操作的稳定性。
车辆主动悬架模型的运动方程即：
对于被动悬架和主动悬架，选取状态变量，建立被、主动悬架的状态方程，可以较好地反映悬架系统的运动特性，输出变量也可以反映驾驶车辆的平顺性和操纵性。
2 车辆悬架系统仿真实例计算
在MATLAB/Simulink中建立1/4车辆悬架的计算机仿真模型，然后进行被动悬架和主动悬架的性能分析。以某轿车的后悬架为例，计算各输入参数，如表1所示。
2.1 被动悬架系统仿真
对于被动悬架模型，将各参数代入被动悬架系统方程，在MATLAB中输入命令[z，p，k]=ss2zp（A，B，C，D），求出被动悬架系统的闭环特征根：
极点均位于左半平面，该系统为最小相位系统，车辆被动悬架系统是稳定的。
2.2 主动悬架系统仿真
对于主动悬架模型，需要获取系统的制动力。先求出系统的状态变量X，求出反馈系数K，将二者相乘，得到制动力U。为使系统可以快速响应，控制信号的加权系数R取1，qa=80 000，qb=5，所以Q=[80000 0 0 0；0 0 0 0；0 0 5 0；0 0 0 0]，在MATLAB中输入命令[K，P，E]=LQR[A1，B1，Q，R]，可得：
K=[282.84 424.83 -277.37 -4.01]
原状态方程可以写成：
X=（A1-B1K）X+D1w（t）（11）
Y=（C1-EK）X（12）
将各参数代入主动悬架方程，在MATLAB中输入命令[z，p，k]=ss2zp（A，B，C，D），可以求出主动系统的闭环特征根：
极点均位于左半平面，符合系统稳定的条件，车辆主动悬架系统是稳定的。
2.3 仿真分析与对比
在MATLAB/Simulink建立被动悬架模型和主动悬架模型的计算机仿真示意图如图3、4所示。
模拟路面时，白噪声信号作为路面不平整度的输入。仿真模块输入为有限带宽白噪声，经过一次积分后可得到仿真路面。
人体在感知车辆的平顺性和舒适性时，体现在对车体本身振动的频率的感受，即车身加速度。车辆被、主动悬架系统仿真时域变化曲线如图5~图7所示。图5所示为车身加速度，图6为悬架动挠度，图7为轮胎动载荷。
仿真条件下，将车辆被、主动悬架系统作对比。计算出两个系统的性能指标的均方根值如表2所示。
由表2可以看出，在车轮动载荷基本相同的情况下，所设计的车辆主动悬架降低了车身加速度，与被动悬相比较，其均方根值减少了17%，悬架动挠度也较好地控制在可接受的范围之内。结果表明车辆的平顺性和稳定性有一定的提高。人们乘坐车辆的舒适性可有较好的改善。
3 结束语
悬架系统是连接车身与车轮之间所有传递力装置的总称，其性能的好坏关乎汽车的操纵稳定性和行驶的平顺性，设计性能较好的悬架系统已成为现代车辆研究的关键。传统的设计方法，汽车悬架系统设计和开发周期长，且成本高。用计算机辅助设计和控制理论方法来完成悬架系统的设计己成为当今工厂、企业普遍采用且行之有效的方法，可大大节省产品成本。
本文对1/4车模型被、主动悬架系统进行了分析，对1/4车模型的被、主动悬架系统进行数学模型的推导以及仿真模型的建立。主动悬架相对于被动悬架系统主要区别在于主动控制器的设计，本文主要依据最优控制原理，对1/4车模型主动悬架控制器来进行设计，使其性能相对于1/4车模型被动悬架系统有较大的改善。从仿真实验结果来看，主动悬架的各项性能指标均优于被动悬架。
参考文献
[1] 张海涛.基于半车模型的主动悬架控制器设计与仿真[D].芜湖：安徽工程大学，2012.
[2] 王望予.汽车设计[M].北京：机械工业出版社，2000.
[3] 孙义杰，巢凯年.ADAMS/VIEW在汽车前悬架仿真应用及优化分析[J].西华大学学报，2005，24（6）：13-17.
[4] 孙殿柱，王丰元.当前CAD技术的发展趋势[J].机械，1998，25（6）：47-48.
[5] 曹观波.汽车前悬架系统建模仿真与分析[D].长春：吉林大学，2012.