卡诺图是化简逻辑用的一种比较简单的图形方法 , 适用于 几个变量的逻辑运算(少于 5 、 6 个)。
可用于逻辑化简,逻辑极小化,使表达式中乘积项或和项 以及变量数目最小。
把逻辑函数的真值表相应的填入一个特定形式的方格内, 就得出逻辑函数的卡诺图。
卡诺图是一个由多个小方块组成的方框。每个小方块用于 一个最小项。当从一个小方块移到其相邻的小方块时,已 有一个变量被取非。
“ 相邻 ” 包括每行,每列的两端
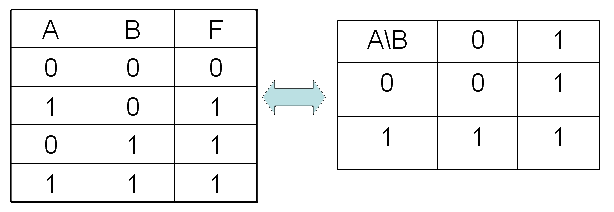
F = A+B 真值表 F = A+B 的卡诺图
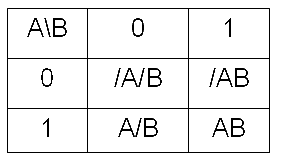
二变量卡诺位置图

填入最小项的二变量卡诺图
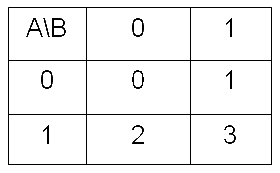
二变量卡诺位图
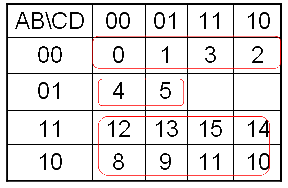
四变量卡诺位置图
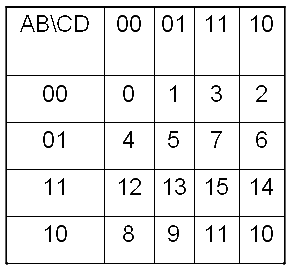
四变量卡诺图
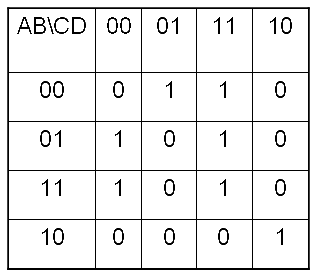
从三变量逻辑函数 Z=AC+AB/C 画卡诺图真值表填图
先把 Z 函数化为最小项表达式 – Z = AC+AB/C = ACB+/B) +AB/C = ABC+A/BC+AB/C
由表达函数表示:
![]()
卡诺位置图
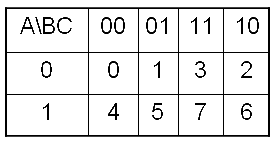
卡诺图

若是逻辑函数表示最小项的列表形式,则在相应的方块中填 1 ,其它填 0 。
若是逻辑函数表示最大项的列表形式,则应在相应的方块中 填 0 ,其它填 1 。
无关变量用 X 表示,它可以为 1 ,也可为 0 ,取决于是否能将 逻辑简化得更好形式。
如: F(A,B,C)=m(0,1,5,7)
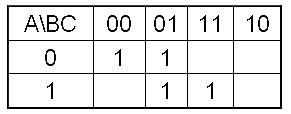
或 F(A,B,C)=M(2,3,4,6 )
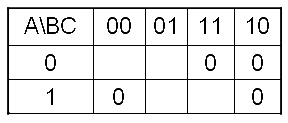
用卡诺图简化逻辑表达式
相邻小方格所代表的最小项之和可合并为一 项,且可消除一个变量。 “ 相邻 ” 包括每行, 每列的两端。
简化步骤:先将孤立为 1 的的小方格圈起 来,再将两个相邻为 1 的方格圈起来,然后 是 4 个, 8 个 ….2 n 个圈起来。
逻辑简化的关键:适当的圈相邻的方格群, 圈数应画的最少,而圈应尽量的大。
如: l Y = /A/B/C/D+/A/B/CD+/A/BCD+/A/BC/D=/A/B – Y = /AB/C/D+/AB/D = /AB/C – Y = Y(8,9,10,11,12,13,14.15) = A