边境安全监视、重要设施防护和交通流量控制等市场需求,极大地开拓了地面雷达应用领域,使其受到越来越广泛的重视。实际环境中,慢速目标(例如人员)是威胁度较高的一类目标,对其检测能力成为衡量雷达系统性能的重要指标。而现实中受地杂波的影响,多数雷达对沿其径向速度较慢的目标,面临检测能力不足的问题。主要原因包括:首先,相对于快速运动目标,慢速目标在多普勒域与地物杂波谱存在更为严重的交叠,很难从地物杂波中对其进行有效提取。其次,以行人为典型的地面慢速目标,多为弱小目标,具有机动性强、反射系数小但RCS起伏大的特点,明显影响了对其的有效检测。
运动平台下的慢速目标检测,常采用偏置相位中心天线(DPCA)和空时自适应处理(STAP)技术,但均难以直接用于地面雷达。目前,常用方法主要是由MTI滤波器抑制地物静止杂波,然后采用灵敏度高的恒虚警检测方法,如ML-CFAR、OS-CFAR、OSGO-CFAR等。但受系统指标限制,MTI滤波器阶数不能设计过高,其较宽的过渡带导致对宽谱地物杂波抑制中不可避免损失了目标能量。但以上算法在提高慢速目标检测概率的同时,虚警率增加较快,对系统的性能提升有限。部分文献提出了杂波图检测慢速目标的思想,并引起较大关注,但有关其具体应用情况却报道较少。本文将杂波零频抑制和改进的杂波图,用于地面慢速目标检测,以提高雷达对地面目标的探测能力。
1 基本原理
1.1 零多普勒频率抑制
通常而言,地物杂波为静止回波,能量集中在零多普勒频率附近,具有双边对称特点。较为恶劣的情况下,杂波均方根谱宽约0.37m/s (折合为速度值表示),而强度通常高于系统热噪声60 dB以上。以人员这类慢速弱小目标为典型地面慢速目标分析,其速度范围在0.3~1.5 m/s。为实现地面慢速目标的有效检测,首先要考虑地杂波的抑制,即零多普勒频率附近的窄带谱能量抑制问题。这种零频抑制的滤波器应在零多普勒频率处呈现深的止带凹口,而随着频率的增加呈现快速的上升斜率,以保证慢速目标的检测能力。
对于FIR数字滤波器,通常需要数十甚至上百阶才能满足要求。而Kalmus滤波器则具备这一特点。它由两个共轭关系的复数滤波器实现,其滤波器传输函数可以表示为式(1)。因此,地杂波零频抑制可通过设计Kalmus滤波器完成。
Hkamus(f)|=||H(f)|-|H*(f)| (1)
1.2 杂波图检测
杂波图检测的基本思想是利用杂波和目标回波的时间积累特性不同,完成二者的有效分离。相比基于空间平滑估计杂波背景的CFAR算法,杂波图更好地利用了杂波的时间分布特性。而杂波图的一阶递归滤波方式如图1所示。
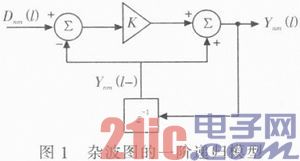
其中,l表示天线扫描周期,一次扫描得到的杂波单元幅度是Dnm(l),已知杂波图值为Ynm(l-1),通过下式可以得到新的杂波图值Ynm(l)。
Ynm(l)=(1-K))Ynm(l-1)+KDnm(l) (2)
K是小于1的衰减因子,多次更新之后就可以得到杂波的平均幅度。当K值取较小值,杂波图需长时间积累平稳,适用于随时间变化缓慢的杂波背景。较大K值则用于适应环境杂波急剧变化情况。
2 慢速目标检测
雷达波束照射区内的地面不仅有大量的散射单元,还存在强的点状散射单元,如城市楼房、水塔等。地杂波概率密度函数将趋向于莱斯分布,可表示为:
![]()
式中,Io为零阶贝塞尔函数,σ2为代表地杂波起伏分量的平均功率,μ为强散射点的回波幅度,为低频直流分量。当μ=0时,则恢复为瑞利分布。
通过零频抑制去除地杂波低频直流分量,可使Rice杂波转换为瑞利杂波。然后对慢速目标与杂波剩余的多普勒交叠区,进行杂波图CFAR可以改善检测性能。基于零频抑制和杂波图的慢速目标检测主要由两部分组成,如图2所示:1)地杂波零频抑制;2)杂波剩余的时间平滑,即杂波图CFAR。
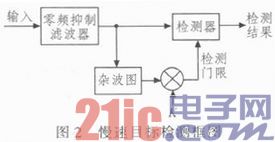
3 Kalmus滤波器设计
Kalmus滤波器传输函数由式(1)表示,其中|H(f)|项可以通过与离散傅里叶变换等效的横向滤波器实现。由DFT定义可以推导出其等效为一组滤波器组,其响应函数为
![]()
其中,0≤k≤N-1表示滤波器组的组号。Kalmus滤波器本质是将DFT滤波器组中的相邻两个滤波器相减以获得深的凹口,然后通过频域搬移使凹口落在零频。由此可得到Kalmus滤波器的幅频响应,如图3所示。
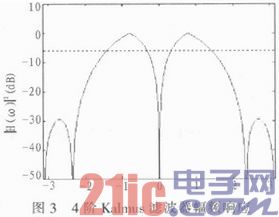
按照上述方式,两个滤波器的系数可以设计为
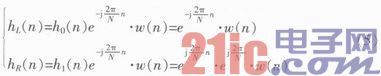
其中,N代表滤波器阶数,且0≤n≤N,w(n)为长度为N的窗函数。此外,Kalmus滤波器存在一定旁辦,可通过窗函数法进行加权抑制。
4 改进的杂波图检测
普通杂波图对慢速目标检测,通常面临不连续的问题。这是由于杂波图更新频率过快,与目标通过距离单元的时间不匹配造成的。假定雷达系统的距离单元大小为L,慢速目标以速度v通过距离单元的时间为t=L/v。假定杂波图更新频率远小于t,则在t时间内目标一直位于该距离单元内。杂波图积累将多次采用目标能量,造成杂波背景估计偏差。最终对目标的检测结果,表现为数次检测后目标消失;而目标运动至下一单元后,又将重复这一过程。

杂波图检测的改进包括以下方面:1)杂波图更新频率可设,使其与距离单元通过时间匹配。2)检测后标记目标和背景单元,目标单元不参与杂波积累。3)采用邻域的背景单元插值计算目标单元背景,即空间邻域插值。改进的方法框图如图4所示。
5 仿真实验
5.1 Kalmus滤波器性能仿真
为设计性能适用的零频抑制滤波器,对不同阶数下Kalmus滤波器的半功率点位置进行了仿真实验。

图5为半功率点起点和终点位置随阶数的变化曲线,所加窗为Hanning窗。滤波器半功率点起点位置随着阶数增加减小,但高阶滤波器起点位置减小不再明显。本文采用8或16阶。另外,加窗抑制旁辦也在一定程度上增加了通带范围。
5.2 慢速目标检测仿真
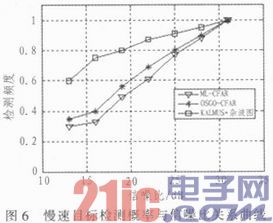
通过模拟强杂波环境下的慢速目标检测过程,验证检测性能。其中,模拟杂波高于系统噪声60 dB,目标运动速度0.5m/s,信噪比变化13-30 dB。图6为不同方法下统计慢速目标检测概率随信噪比的变化曲线。可以看到,基于零频抑制与杂波图的地面慢速目标检测,性能明显优于其他方法。
6 结束语
慢速目标检测是地面雷达系统中的技术难点。杂波抑制和目标检测方法相结合的设计方式,提供了较好技术途径。基于零频抑制与杂波图的地面慢速目标检测方法,在杂波抑制和目标检测两方面进行了改进,其检测概率改善明显。该方法对提高地面雷达性能具有参考意义。
