一、 电磁场实验定律的总结
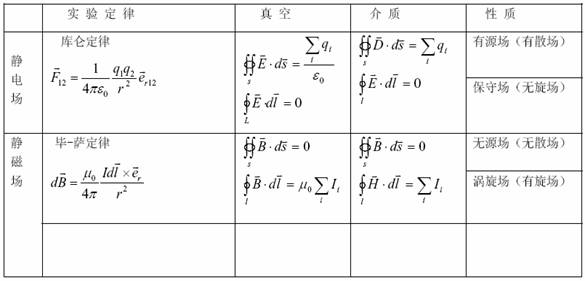
变化的电磁场, 规律——推广; 方程——修正。
变化的磁场:产生感生电场(涡旋电场) 麦克斯韦提出
感生电场的场方程:
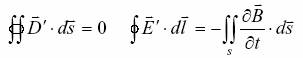
一般情况:空间总电场

变化磁场:产生涡旋电场。------麦克斯韦关于电磁理论的一个假设。
电场的概念加以推广,静电场的方程要加以修正。
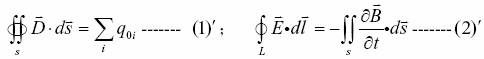
变化电场:是否要产生磁场?磁场的方程是否要修正?
二、位移电流
静磁场的安培环路定理不适用于非稳恒情况
麦克斯韦提出:变化的电场——等效为一种电流(位移电流)——产生涡旋磁场。这是麦克斯韦关于电磁理论的第二个基本假设。
位移电流密度:
![]()
位移电流强度:
![]()
全电流密度:
![]()
全电流
![]()
位移电流与传导电流比较:
相同处:按同一方式激发磁场(涡旋磁场)。
区别:(1)、前者取决于电场的变化,后者由电荷的宏观移动引起。
(2)、前者可以在导体、介质、真空存在;后者在导体中通过。
(3)、前者无焦耳热;后者有焦耳热。
磁场的概念推广了,方程加以修正:
高斯定理:
![]()
环路定理:
![]()
三、麦克斯韦方程组
1、积分形式

2、微分形式
以上方程中既有电学量又有磁学量,说明随时间变化的电场和磁场是不可分割地联系在一起的;若场矢量不随时间变化,则方程就分成两组独立的方程,一组为静电场方程,一组为静磁场方程。
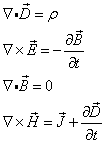
3、麦克斯韦方程组的物理意义:
a、通过任意闭合面的电位移通量等于该曲面所包围的自由电荷的代数和。
b、电场强度沿任意闭曲线的线积分等于以该曲线为边界的任意曲面的磁通量对时间变化量的负值。
c、通过任意闭合面的磁通量恒等于零。
d、磁场强度沿任意闭合曲线的线积分等于穿过以该曲线为边界的曲面的全电流。
物理学家费曼认为,麦克斯韦方程是一座漂亮大厦,以上方程形式美,但并不完全对称,不对称的根本原因是自然界存在电荷却不存在磁荷。磁单极子不存在。
4、麦克斯韦方程组在电磁学中的地位
电和磁现象的最初发现,可以追溯到很古老的历史,但直到十九世纪,麦克斯韦才在前人成就的基础上把各种试验规律总结提高并加以发展,成为以麦克斯韦方程为中心的完整的理论体系。麦克斯韦方程组在电磁学的地位和作用与牛顿运动定律在经典力学中的地位和作用相当。
5、适用范围:
麦克斯韦电磁场理论是从宏观的电磁现象总结出来的经验定律,和牛顿经典力学一样只在宏观试验所能达到的范围内适用。高速领域——麦克斯韦方程仍正确。可用它来研究高速运动电荷所产生的电磁场及一般辐射问题。微观领域——麦克斯韦方程不完全适用。罗伦兹把它推广到分子和原子的微观领域,创立了电子论,对电磁现象作了微观解释,取得了一些成绩,但也遇到了不可克服的困难,因而现代发展了更普遍的量子电动力学。
宏观电磁理论可以看作量子电动力学在某些特殊条件下的近似规律,正象牛顿经典力学是相对论力学在低速下的近似规律一样,都是在一定条件下的相对真理。
