19世纪40年代,由于电气技术发展的十分迅速,电路变得愈来愈复杂。某些电路呈现出网络形状,并且网络中还存在一些由3条或3条以上支路形成的交点 (节点)。这种复杂电路不是串、并联电路的公式所能解决的。
1845年,刚从德国哥尼斯堡大学毕业、年仅21对的基尔霍夫在他的第一篇论文中提出了适用于网络状电路计算的两个定律,即著名的基尔霍夫定律。这两个定律分为基尔霍夫第一定律和基尔霍夫第二定律,其中基尔霍夫第一定律称为基尔霍夫电流定律,简称KCL;基尔霍夫第二定律即为基尔霍夫电压定律,简称KVL。
这组定律能够迅速地求解任何复杂电路,从而成功地解决了这个阻碍电气技术发展的难题。
下面,从基尔霍夫第一定律和基尔霍夫第二定律展开深入探讨,加以例题详解,希望读者朋友们能对基尔霍夫定律有一个更深入的理解。
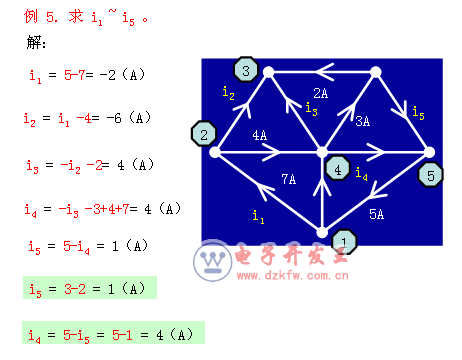
一、基尔霍夫电流定律(KCL)例题
在集总电路中,在任一时刻,流入任一节点的电流等于由该节点流出的电流。或者说,在任一瞬间,一个节点上各支路电流的代数和恒为 0。
即:∑Ι=0

基尔霍夫电流定律的依据:电流的连续性(电荷守恒)。

基尔霍夫电流定律的扩展:
基尔霍夫电流定律还可以扩展到电路的任意封闭面。
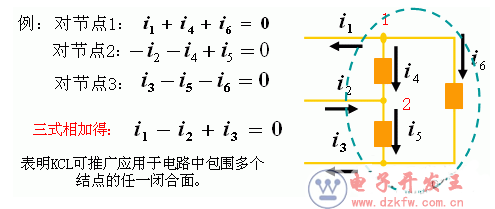
明确:
(1) KCL是电荷守恒和电流连续性原理在电路中任意结点处的反映;
(2) KCL是对支路电流加的约束,与支路上接的是什么元件无关,与电路是线性还是非线性无关;
(3)KCL方程是按电流参考方向列写,与电流实际方向无关。
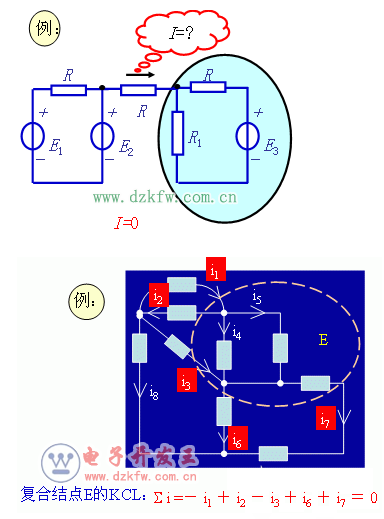
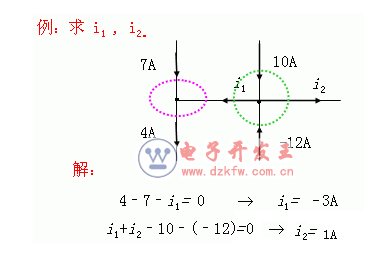
思考:
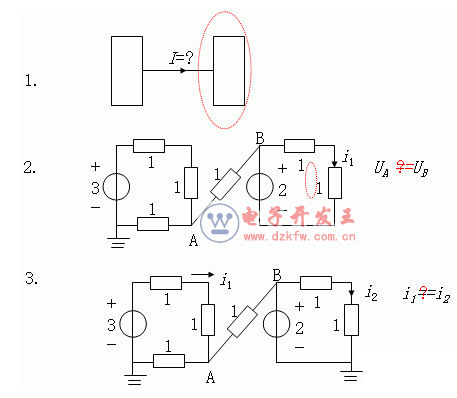
二、基尔霍夫电压定律(KVL)例题
在集总参数电路中,任何时刻,沿任一回路,所有支路电压的代数和恒等于零。即:
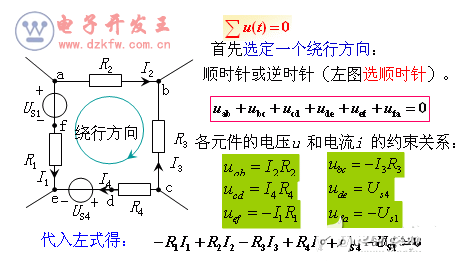
电压源的参考方向与回路绕行方向关联, 取正;反之取负。
电阻电流 的参考方向与回路绕向相同时,IR为正,反之取负。
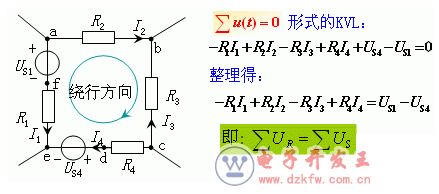
电阻压降 电源压升
KVL方程常用该式表示。
(1)US的参考方向与回路绕向非关联时,放在等号右边取正,反之取负。
(2)电阻电流 的参考方向与回路绕向相同时,IR 为正,反之取负。
基尔霍夫电压定律(KVL)的扩展:
基尔霍夫电压定律也适合开口回路。
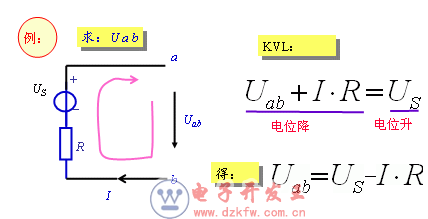
KVL也适用于电路中任一假想的回路。
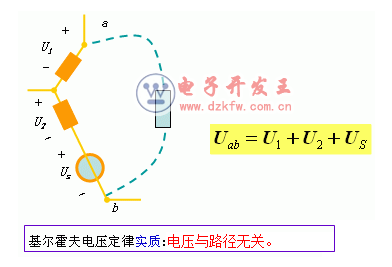
推论:电路中任意两点间的电压等于两点间任一条路径经过的各元件电压的代数和。元件电压方向与路径绕行方向一致时取正号,相反取负号。
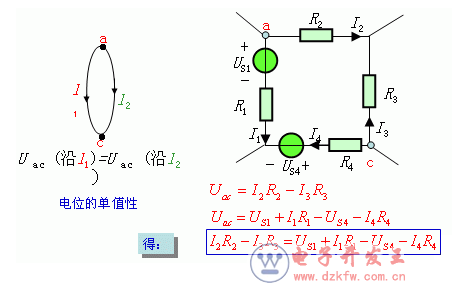
KCL、KVL小结:
1.KCL是对支路电流的线性约束;KVL是对支路电压的线性约束。
2.KCL、KVL与组成支路的元件性质及参数无关。
3.KCL表明在每一节点上电荷是守恒的。
KVL是电位单值性的具体体现(电压与路径无关)。
4.KCL、KVL只适用于集总参数的电路。
5.只要是集总参数电路,无论元件是线性还是非线性、是时变还是非时变的,KCL、KVL总是成立的。
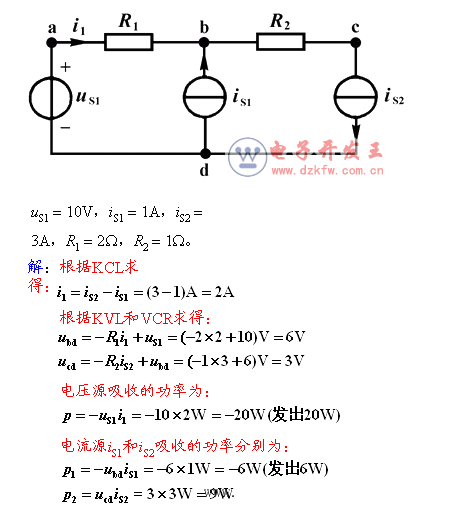
例6. 电路如图所示。已知uS1 = 10V,iS1= 1A,iS2 = 3A,R1 = 2?,R2 = 1?。求电压源和各电流源吸收的功率。
例7. 如图所示电路中,R1=1Ω,R2=2Ω,R3=3Ω,US1=3V,US2=1V 。求电阻R1两端的电压U1。

方法2:

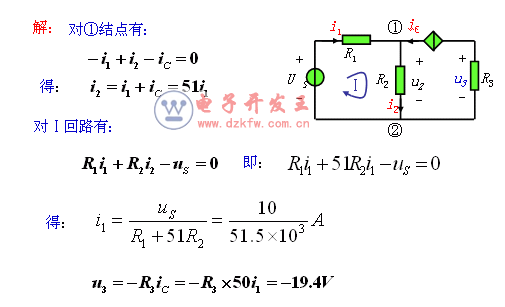
例8. 如图,已知R1=0.5kΩ,R2=1kΩ,R3=2kΩ,uS=10V,电流控制电流源的电流iC=50i1。求电阻R3两端的电压u3。