一、叠加定理
图 4.1-1 （ a ）所示电路中，有两个激励，即独立电压源 
和独立电流源 
，现欲求 R1 支路上的电流 
。
用网孔电流法求解。设网孔电流分别为 
，其方向都为顺时针方向，如图 4.1-1 （ a ）所示。网孔方程为
解方程得，网孔电流为
所以， R1 支路电流为
其中， 
可以看成是当 
时的 
的值， 
则可看成是当 
时的 
的值。如图 4.1-1 （ b ）、（ c ）。
令
则
其中， k1 ， k2 是由电路的结构和元件的参数决定的。对于线性电路， R1 、 R2 、 R3 都是常数，不会随着电路中激励的数目和大小的改变而改变，所以 k1 ， k2 也不会随激励的改变而改变，即为常数。 i 是激励的一次线性函数。
叠加定理
（ superposition theorem ）
由线性元件组成的线性电路，当 n 个激励共同作用时，在某条支路上产生的响应，等于各个激励单独作用时产生的响应的代数和。
其中， 
表示 n 个激励（独立电压源或独立电流源）， r 表示某条支路上产生的响应（电压或电流）。 
都是常数，其大小由电路的结构和元件的参数决定。
应用叠加定理时应注意的问题
1 ．叠加定理是线性电路的一个重要性质，因此只适用于线性电路，对于非线性电路则不能使用。
2 ．当某个激励单独作用时，其他激励均取 0 。将独立电压源取 0 ，是把电压源短路，将独立电流源取 0 是把电流源开路。
3 ．受控源虽然带有电源的性质，但不直接起激励作用，因此，在叠加定理中，受控源一般不单独作用，而是把受控源当电路元件处理。当独立源单独作用时，受控源应保留在电路中。
4 ．叠加定理只适用于计算电压或电流，而不适用于计算功率，因为功率与电压、电流之间的关系不是线性关系。
例 4.1-1 图 4.1-2 （ a ）所示电路，试用叠加定理求 3 Ω电阻上的电压 U 及功率。
解：电路中有两个独立源共同激励。
1 、当 12V 电压源单独激励时，电流源应视为 0 ，即把电流源开路，如图 4.1-2 （ b ）所示。
由分压公式，得
 |
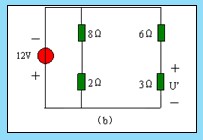2 、当 3A 电流源单独激励时，电压源应视为 0 ，即把电压源短路，如图 4.1-2 （ c ）所示。对图 4.1-2 （ c ）电路作变换，得图 4.1-2 （ d ）所示电路。
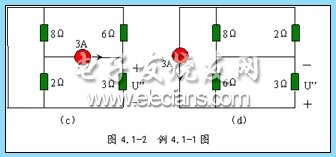
3 、当电压源和电流源共同作用时，由叠加定理得 3 Ω电阻上的电压
3 Ω电阻上的功率为
注 意
计算功率时，不能用叠加定理。
例 4.1-2 用叠加定理计算图 4.1-3 （ a ）所示电路中受控源两端电压及功率。
 |
解：当 4V 电压源单独作用时，电流源视为开路，其电路如图 4.1-3 （ b ）所示，对图中所示的回路，利用 KVL ，得
所以，
则
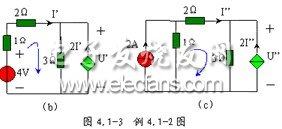
当 2A 电流源单独作用时，电压源视为短路，其电路如图 4.1-3 （ c ）所示，对图中所示的回路，利用 KVL ，得
所以，
则
因此，当电压源和电流源共同作用时，利用叠加定理得
受控源两端电压为
受控源的功率为
二、齐次定理
齐次定理
（ homogeneity theorem ）
当线性电路中只有一个独立源作用时，电路的响应与激励成正比。
推 论：对于线性电路，若所有激励同时扩大（或缩小） K 倍，则电路中任一支路的响应也扩大（或缩小） K 倍。
例 4.1-3 图 4.1-4 所示的梯形电路中， Us=6V ，试用齐次定理计算支路电流 I5 。
解：这个电路是由电阻的串、并联组成，可以用等效电路的分析方法进行计算，但是用齐次定理计算会更方便。先设 I5 支路电流为 
，则
所以，
故
根据齐次定理，激励 
与响应 
成正比，即
因此，
注 意
应用叠加定理和齐次定理时，当激励的参考方向反向时，相当于激励变为原来的－ 1 倍。
例 4.1-4 图 4.1-5 所示电路中， N 是不含独立源的线性网络，有 3 个独立源共同激励， a 、 b 两端的电压 
为 10V 。当电压源 
和电流源 
反向而 
不变时， 
变为 5V ；当电压源 
和电流源 
反向而 
不变时， 
变为 3V 。试问：只有电流源 
反向而电压源 
和 
不变时， 
变为多少？
解：由于是线性电路，所以可用叠加定理。 3 个独立源共同激励，电路的响应
（ 1 ）
式中， 
为常数，由电路的结构和元件的参数决定。
当电压源 
和电流源 
反向而 
不变时，电路的结构和元件的参数不变， 
的大小不变，而 
都要乘以系数－ 1 ，这时的 a 、 b 两端的电压为
（ 2 ）
又当电压源 
和电流源 
反向而 
不变时， 
乘以系数－ 1 ， a 、 b 两端的电压为
（ 3 ）
(2) ＋ (3) ，得
（ 4 ）
所以，当只有电流源 
反向而电压源 
和 
不变时， a 、 b 两端的电压为
