一、网孔电流方程
出发点
进一步减少方程数，用未知的网孔电流代替未知的支路电流来建立方程。
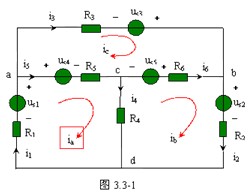
图3.3-1所示电路，共有n=4个节点，b=6条支路（把电压源和电阻串联的电路看成一条支路）。显然，独立的网孔数为b－n＋1=3个。
1、网孔电流
设想每个网孔中有一个假想的电流沿着构成该网孔的各条支路循环流动，把这一假想的电流称为网孔电流（mesh current），如图3.3-1中的
分别表示网孔a、b、c的网孔电流。电路中各支路电流就可以用网孔电流表示
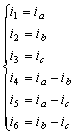
结 论：用3个网孔电流表示了6个支路电流。进一步减少了方程数。
2、网孔电流方程
根据KVL，可得图3.3-1电路的网孔电流方程
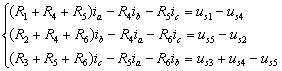
网孔电流方程的一般形式
自电阻×本网孔电流±Σ（互电阻×相邻网孔电流）= 本网孔中沿网孔电流方向的所有电压源的电位升之和
自电阻（self resistance）是各网孔中所有支路电阻之和，互电阻（mutual resistance）是两个相邻网孔之间的共有电阻。第二项前的正负号由相邻网孔电流与本网孔电流在互电阻上流过的方向是否一致来决定，若一致取正号；反之取负号。
网孔电流法分析电路的一般步骤
确定电路中的网孔数，并设定各网孔电流的符号及方向。按常规，网孔电流都取顺时针或逆时针方向。列写网孔电流方程，并求解方程，求得各网孔电流。由求得的网孔电流，再求其他的电路变量，如支路电流、电压等。
例3.3-1 图3.3-1所示电路中，已知us1=21V，us2=14V，us3=6V，us4=us5=2V，R1=3Ω，R2=2Ω，R3=3Ω，R4=1Ω，R5=6Ω，R6=2Ω，求各支路电流。
解：1. 电路的网孔为3个。设定3个网孔电流的符号及方向如图3.3-1所示。
2．列写网孔方程
网孔a： 
网孔b： 
网孔c： 
代入参数，并整理，得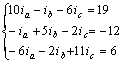
解得网孔电流为： 
3．由网孔电流求各支路电流
2、全欧姆定律
只有一个网孔的电路，称为单回路电路（single loop circuit）。对于单回路电路，有全欧姆定律。
全欧姆定律：对于单回路电路，回路电流i等于沿回路电流方向的所有电压源的电压升的代数和除以回路中所有电阻之和。
二、含有电流源的电路
1、有伴电流源
结 论：如果电路中的电流源是有伴电流源，将有伴电流源等效成有伴电压源。
方法一 把电流源当电压源处理
设定电流源两端的电压，列写网孔方程，利用电流源的电流与网孔电流之间的关系再补充一个方程。
2、无伴电流源
电流源处于边界支路上
结 论：电流源所在网孔的网孔电流即为电流源的电流，因此可以少列一个网孔方程。
例3.3-2 图3.3-2所示电路中，试用网孔电流法求流过3Ω电阻的电流I1。
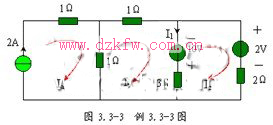
解：电路中含有一个2A电流源，处于网孔a的边界支路上。取顺时针方向为各网孔电流的方向，则
（1）
因此，只需列写两个网孔方程，
网孔b： 
（2）
网孔c： 
（3）
经整理后，得
解得网孔电流为： 
所以，流过3Ω电阻的电流为
2）电流源处于相邻网孔的公共支路上
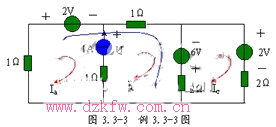
例3.3-3 电路如图3.3-3所示，试用网孔电流法求各网孔电流。
解：电路中的1A电流源处于网孔a、b的公共支路上。设它的两端电压为U，并将它当作电压源看待，列写网孔方程，
网孔a： 
（1）
网孔b： 
（2）
网孔c： 
（3）
补充方程： 
（4）
整理后得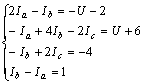
解上述方程组，得网孔电流为
方法二 超网孔（super mesh）方法
把以电流源为公共支路的两个网孔当作一个超网孔处理，使电流源所在支路不出现在超网孔的支路中。
注 意：列写超网孔方程时，由于电流源与1Ω电阻串联的支路没有出现在超网孔中，所以，这条电流源支路不应计算进去。
利用超网孔的方法计算例3.3-3。
对超网孔： 
（1）
对网孔c： 
（2）
补充方程： 
（3）
整理后得，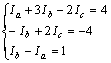
解方程组，得网孔电流为
三、含有受控源电路
思 路：把受控源当独立源看待。当然，如果受控源的控制量不是网孔电流，应再补充一个能反映控制量与某网孔电流之间关系的方程式。
例3.3-4 电路如图3.3-4所示，试网孔电流法求受控源发出的功率。
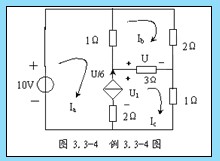
解：电路中有一个受控电流源，而且是无伴电流源，设其两端电压为U1，把它当独立的电压源看待。
设3个网孔的网孔电流分别为
，其方向均为顺时针方向，如图3.3-5所示，列写网孔方程，
网孔a： 
（1）
网孔b： 
（2）
网孔c： 
（3）
补充方程： 
（4）
（5）
以上5个方程联立求解，得
受控源的电流为 
所以，受控源发出功率为