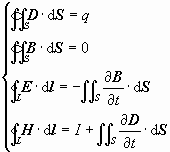
这是1873年前后，麦克斯韦提出的表述电磁场普遍规律的四个方程。
其中：（1）描述了电场的性质。在一般情况下，电场可以是库仑电场也可以是变化磁场激发的感应电场，而感应电场是涡旋场，它的电位移线是闭合的，对封闭曲面的通量无贡献。
（2）描述了磁场的性质。磁场可以由传导电流激发，也可以由变化电场的位移电流所激发，它们的磁场都是涡旋场，磁感应线都是闭合线，对封闭曲面的通量无贡献。
（3）描述了变化的磁场激发电场的规律。
（4）描述了变化的电场激发磁场的规律。
变化场与稳恒场的关系：当
时，方程组就还原为静电场和稳恒磁场的方程：
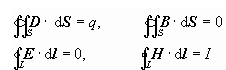
在没有场源的自由空间，即q=0, I=0，方程组就成为如下形式：
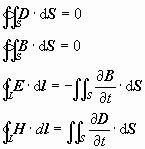
麦克斯韦方程组的积分形式反映了空间某区域的电磁场量(D、E、B、H)和场源(电荷q、电流I)之间的关系。