根据第一章中介绍的图论知识可知，实际电路结构可用一个有向图来具体描述。如某一电路的有向图如图7-2-1所示，把有向图各节点和支路编号，然后依次把各支路与相应连接点的连接信息用数字形式记忆下来。根据这些信息可完整描述电路的联接关系，若把这些信息输入计算机，则计算机就会根据这些信息自动识别电路关系，并应用基尔霍夫定律建立相应的电路方程，进行相应的运算。
图 7-2-1
电路中支路与节点的连接关系可用关联矩阵来描述。设电路的节点数为
，支路数为b。依次给节点和支路编号（节点编号用一圆圈加以区别），然后把有向图用一个
阶矩阵来表示，记为
。矩阵的行对应于有向图的节点，矩阵的列对应于网络的支路。中的元素
作如下定义：
（7-2-1）
式中，称为电路的节点—支路关联矩阵。例如对于图7-2-1所示的电路，可写出关联矩阵为：
关联矩阵的每一列对应于一条支路，每一支路必连接于二个节点，且方向为一进一出。因此的每一列中只包含二个非零元素＋1和－1，如上面关联矩阵所示。如果把所有行的元素按列相加，则得到全零的行，因此矩阵的行不是彼此独立的。对于中任一行元素可以通过把除该行以外的所有行相加并变号而获得。
如果把的任一行划去，剩下的矩阵为
阶矩阵
，记作A。由上分析可知，用该新矩阵A来代替同样能充分描述有向图的连接关系，矩阵A称为降价关联矩阵，划去的行对应的节点即为参考节点，上图中若以节点④为参考点，则其降价关联矩阵为
在实际应用中通常采用降价关联矩阵形式，因此在一般叙述中往往略去“降价”二字。关联矩阵可由给定的网络有向图得出，同样当给定关联矩阵A后也可推导出它所代表的有向图。
关联矩阵A的每一行是相互独立的，每行之间是线性无关的，A的秩等于矩阵的行数
。实际上由A的元素的定义可知，关联矩阵的每一行反映了该节点的电流平衡关系式。A中线性独立的n行代表了网络中
个节点的电流平衡关系。
下面分析关联矩阵A与支路电流，支路电压，节点电位之间的关系。设网络各支路电流为
，支路电流方向与有向图支路方向一致，用矩阵形式表示的支路电流列向量为
。
若用关联矩阵A
左乘支路电流列向量i，可得一n行的列向量矩阵。由关联矩阵的定义可知，该列向量中每一行的元素之和恰为离开该节点的支路电流与流入该节点的支路电流之代数和，且离开节点时电流为正，流入节点时电流为负。由基尔霍夫节点电流定律可知，节点电流代数和恒为零。因此可得A左乘i后其值为零向量，即有：
（7-2-2）
该式反映了网络各节点的电流平衡关系，称为矩阵形式的基尔霍夫电流定律。对于正弦稳态交流电路分析，上式可写为：
（7-2-3）
对于图7-2-1所示的网络，设支路电流列向量为
，该网络的关联矩阵已写出，用A左乘i可得：
由式可见，
的乘积列向量其实为n个节点的KCL方程式。
在用节点电压法解题时要用到节点电压与支路电压之间的关系。下面分析节点电压与支路电压之间关系的矩阵形式。设网络各节点电压的列向量为
，（式中为使节点电压与支路电压相区别，在下标中用一加圈数字表示节点），参考节点的电压为零。支路电压列向量为
。若用关联矩阵的转置矩阵
左乘节点电压列向量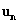
，可得一个b 行的列矩阵。前已指出，A中每一列只包含二个元素（若支路连接于参考节点，则该列只包含一个元素），反映支路所连接的二个节点，且为一正一负，即支路方向离开节点为正，反之为负。因此与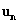乘积的列向量第一行中只包含该支路离开节点的电压与指向节点的电压之差，即为该支路的支路电压值。因此左乘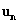的值即为支路电压列向量u，即有：
（7-2-4）
对于正弦稳态交流电路有：
（7-2-5）
对于图7-2-1所示的网络，其节点电压列向量为
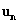，用左乘，得
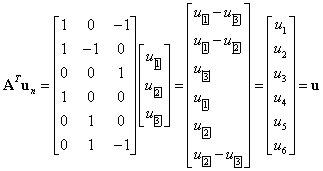
式（7-2-4）反映了节点电压与支路电压之间的关系。