| 高斯定理是一条反映静电场规律的普遍定理,在进一步研究电学时,这条定理很重要。在这里,我们只应用它来计算某些对称带电体所激发的电场中的场强,在这些情况中,它比应用电场强度叠加原理来计算场强要方便得多。下面举例说明高斯定理的这种应用。 (1)在电场强度已知时,求出任意区域内的电荷 (2)当电荷分布具有某种特殊对称性时,用高斯定理求出该种电荷系统的电场分布 |
| 例1:求均匀带正电球体内外的电场分布,设球体带电量为q,半径为R。 |
| 应用电通量的定义和高斯定理联立求解。(解略) |
| 讨论:在球面外(r>R),点P的场强为: |
方向沿半径指向球外(如q<0,则沿半径指向球内)。 |
| 在球面内(r<R),点P的场强为: |
| 综上所述,可得如下结论:均匀带电球面外的场强,与将球面上电荷全部集中于中心的点电荷所激发的场强一样;球面内任一点的场强则为零。均匀带电球面的场强分布,可用其大小E与距离r的关系曲线来表示。这条曲线E-r 在r=R 处是间断的,即场强大小E的分布在该处是不连续的。 |
| 例2:均匀带正电无限长细棒的场强.其线电荷密度为 |
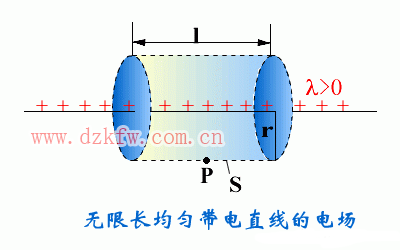 |
| 场强的大小为: |
| 例3:均匀带正电的无限大平面薄板的场强。 |
导读:目前正在解读《高斯定理的应用》的相关信息,《高斯定理的应用》是由用户自行发布的知识型内容!下面请观看由(电工技术网 - www.9ddd.net)用户发布《高斯定理的应用》的详细说明。
提醒:《高斯定理的应用》最后刷新时间 2024-03-14 01:24:38,本站为公益型个人网站,仅供个人学习和记录信息,不进行任何商业性质的盈利。如果内容、图片资源失效或内容涉及侵权,请反馈至,我们会及时处理。本站只保证内容的可读性,无法保证真实性,《高斯定理的应用》该内容的真实性请自行鉴别。
